
【题目】在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。
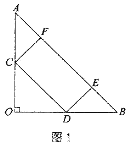
(1)如图1,若C、D恰好是边AO、OB的中点,则此时矩形CDEF的面积为_________;
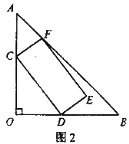
(2)如图2,若![]() =
=![]() ,求矩形CDEF面积的最大值。
,求矩形CDEF面积的最大值。
【答案】(1)S矩形CDEF=16;
(2)矩形CDEF面积的最大值为![]() 。
。
【解析】试题分析:(1)因为当C、D是边AO,OB的中点时,点E、F都在边AB上,且CF⊥AB,所以可求出CD的值,进而求出CF的值,矩形CDEF的面积可求出;
(2)设CD=x,CF=y.过F作FH⊥AO于H.在 Rt△COD中,用含x和y的代数式分别表示出CO、AH的长,进而表示出矩形CDEF的面积,再配方可求出面积的最大值.
试题解析:
(1)如图,当C、D是边AO,OB的中点时,
点E、F都在边AB上,且CF⊥AB。
∵OA=OB=8,
∴OC=AC=OD=4。
∵∠AOB=90°,
∴CD=4![]() 。
。
在Rt△ACF中,
∵∠A=45°,
∴CF=2![]() ,
,
∴S矩形CDEF=4![]() ×2
×2![]() =16。
=16。
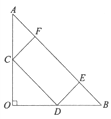
(2)设CD=x,CF=y。过F作FH⊥AO于H。在Rt△COD中,
∵tan∠CDO=![]() ,
,
∴sin∠CDO=![]() ,cos∠CDO=
,cos∠CDO=![]() ,
,
∴CO=![]() x
x
∵∠FCH+∠OCD=90°,
∴∠FCH+∠CDO,
∴HC=y·cos∠FCH=![]() y,
y,
∴FH=![]() y。
y。
∵△AHF是等腰直角三角形,
∴AH=FH=![]() y,
y,
∴AO=AH+HC+CO。
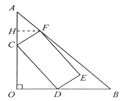
∴![]() ,
,
∴y=![]() (40-4x)
(40-4x)
易知S矩形CDEF=xy=![]()
![]() [(x-5)2-25],
[(x-5)2-25],
∴当x=5时,矩形CDEF面积的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
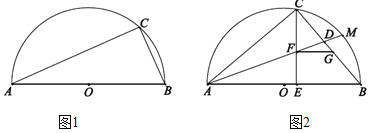
【题目】已知AB是半圆O的直径,点C在半圆O上.
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是![]() 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学生方队,B的位置是第8列第7行,记为(8,7),则学生A在第二列第三行的位置可以表示为( )
A. (2,1) B. (3,3) C. (2,3) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:
①∠AOB=∠COD;
②∠AOB+∠COD= ![]() ;
;
③若OB平分∠AOC,则OC平分∠BOD;
④∠AOD的平分线与∠BOC的平分线是同一条射线,
其中正确的是 . (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两点中,关于y轴对称的是( )
A. (1,-3)和(-1,3) B. (3,-5)和(-5,3) C. (5,-4)和(5,4) D. (-2,4)和(2,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com