练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某自行车行销售、两种品牌的自行车，若购进品牌自行车5辆，品牌自行车6辆，需要进货款9500元，若购进品牌自行车3辆，品牌自行车2辆，需要进货款4500元．

    （1）求、两种品牌自行车每辆进货价分别为多少元；

    （2）今年夏天，车行决定购进、两种品牌自行车共50辆，在销售过程中，品牌自行车的利润率为80%，品牌自行车的利润率为60%，若将所购进的自行车全部销售完毕后其利润不少于29500元，那么此次最少购进多少辆品牌自行车？

    【答案】（1）型车的进价为1000元，型车的进价为750元；（2）最少购进20辆品牌自行车

    【解析】

    （1）首先设型车的进价为元，型车的进价为元，然后根据题意列出二元一次方程组，求解即可；

    （2）首先设购进型车辆，然后根据题意列出不等式，求解即可.

    （1）设型车的进价为元，型车的进价为元．

    解得：

    答：型车的进价为1000元，型车的进价为750元；

    （2）设购进型车辆．

    根据题意，得

    ，

    解得，

    所以型车最少购进20辆．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，CD是△ABC的中线，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中线弧．

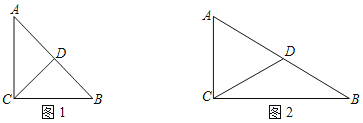
    （1）在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点．

    ①如图1，若∠A＝45°，画出△ABC的一条中线弧，直接写出△ABC的中线弧所在圆的半径r的最小值；

    ②如图2，若∠A＝60°，求出△ABC的最长的中线弧的弧长l．

    （2）在平面直角坐标系中，已知点A（2，2），B（4，0），C（0，0），在△ABC中，D是AB的中点．求△ABC的中线弧所在圆的圆心P的纵坐标t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：y=﹣x+1与x轴，y轴分别交于点A和点B，直线l2：y=kx（k≠0）与直线l1在第一象限交于点C．若∠BOC=∠BCO，则k的值为（　　）

    A. B. C. D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是反比例函数y=图象在第一象限上的一点，连结AO并延长交图象的另一分支于点B，延长BA至点C，过点C作CD⊥x轴，垂足为D，交反比例函数图象于点E．若，△BDC的面积为6，则k=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，平面直角坐标系中，的边在轴的正半轴上，点在第二象限，且，，，抛物线经过点，并与轴交于点，点在抛物线的对称轴上．

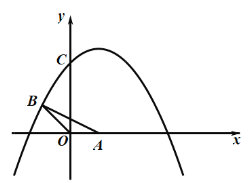
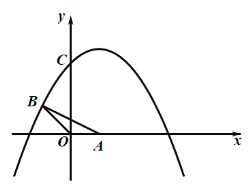
    （图1） （备用图）

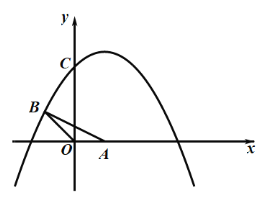
    （备用图）

    （1）求、的值，及抛物线的对称轴．

    （2）求证：以点为圆心，半径为的圆与边相切．

    （3）若满足条件与的点恰好在抛物线上，请求出此时点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC，△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是（ ）

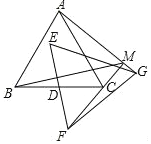
    A.2-B.+1C.D.-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线与x轴交于A，B两点在B的左侧，与y轴交于C，且，

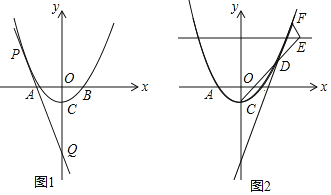
    求c的值；

    是抛物线上一动点，过P点作直线L交y轴于，且直线L和抛物线只有唯一公共点，求的值；

    如图2，E为直线上的一动点，CE交抛物线于D，轴交抛物线于F，求证：直线FD经过y轴上一定点，并求定点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径,点C,D在⊙O上,且AB＝5,BC＝3.

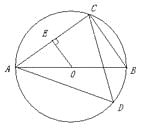
    (1) 求sin∠BAC的值;

    (2) 如果OE⊥AC, 垂足为E,求OE的长;

    (3) 求tan∠ADC的值.(结果保留根号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图甲，直线y=﹣x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．

    （1）求该抛物线的解析式；

    （2）在该抛物线的对称轴上是否存在点M，使以C，P，M为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M的坐标；若不存在，请说明理由；

    （3）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值（图乙、丙供画图探究）．

    查看答案和解析>>

    同步练习册答案