
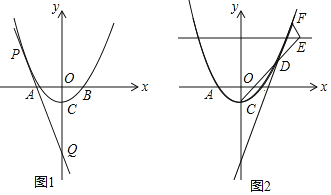
【题目】如图1,抛物线![]() 与x轴交于A,B两点
与x轴交于A,B两点![]() 在B的左侧
在B的左侧![]() ,与y轴交于C,且
,与y轴交于C,且![]() ,
,
![]() 求c的值;
求c的值;
![]() 是抛物线上一动点,过P点作直线L交y轴于
是抛物线上一动点,过P点作直线L交y轴于![]() ,且直线L和抛物线只有唯一公共点,求
,且直线L和抛物线只有唯一公共点,求![]() 的值;
的值;
![]() 如图2,E为直线
如图2,E为直线![]() 上的一动点,CE交抛物线于D,
上的一动点,CE交抛物线于D,![]() 轴交抛物线于F,求证:直线FD经过y轴上一定点,并求定点坐标.
轴交抛物线于F,求证:直线FD经过y轴上一定点,并求定点坐标.
【答案】![]() c=-2;
c=-2;![]() ;
;![]() 证明见解析;直线DF恒过点
证明见解析;直线DF恒过点![]() .
.
【解析】
(1)由题意可知:OC=-c,AB=-2c,令y=0代入抛物线的解析式也可求出AB=![]() ,列出方程即可求出c的值;
,列出方程即可求出c的值;
(2)根据P与Q的坐标求出PQ的直线解析式,然后与抛物线联立方程求出△,令△=0后进行化简,即可求出n与s的值;
(3)设E(a,3),F(a,b),然后求出直线CE的解析式,与抛物线联立方程求出D的坐标,最后求出直线DF的解析式即可求出该定点.
(1)由题意可知:![]() ,
,
![]() ,
,
![]() ,
,
令![]() 代入
代入![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 舍去
舍去![]() 或
或![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
(2)设直线PQ的解析式为:![]() ,
,
将![]() 与
与![]() 代入
代入![]() ,
,
可得: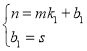 ,
,
解得: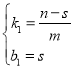 ,
,
![]() 直线PQ的解析式为:
直线PQ的解析式为:![]() ,
,
联立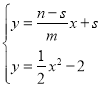 ,
,
化简可得:![]() ,
,
![]() ,
,
![]() 化简可得:
化简可得:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)设![]() ,
,![]() ,
,
设直线CE的解析式为:![]() ,
,
把![]() 和
和![]() 代入
代入![]() ,可得:
,可得: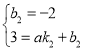 ,
,
解得: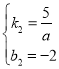 ,
,
![]() 直线CE的解析式为:
直线CE的解析式为:![]() ,
,
![]() 联立
联立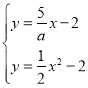 ,
,
解得:![]() 舍去
舍去![]() 或
或![]() ,
,
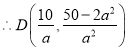 ,
,
设直线DF的解析式为:![]() ,
,
把D和F的坐标分别代入![]() 可得:
可得: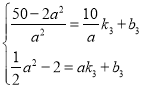 ,
,
解得: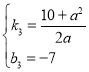 ,
,
![]() 直线DF的解析式为:
直线DF的解析式为:![]() ,
,
令![]() 代入
代入![]() ,
,
![]() ,
,
![]() 直线DF恒过点(0,-7).
直线DF恒过点(0,-7).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,函数![]() (x<0)的图象与直线y=x+2交于点A(-3,m).
(x<0)的图象与直线y=x+2交于点A(-3,m).
(1)求k,m的值;
(2)已知点P(a,b)是直线y=x上,位于第三象限的点,过点P作平行于x轴的直线,交直线y=x+2于点M,过点P作平行于y轴的直线,交函数![]() (x<0)的图象于点N.
(x<0)的图象于点N.
①当a=-1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM结合函数的图象,直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车行销售![]() 、
、![]() 两种品牌的自行车,若购进
两种品牌的自行车,若购进![]() 品牌自行车5辆,
品牌自行车5辆,![]() 品牌自行车6辆,需要进货款9500元,若购进
品牌自行车6辆,需要进货款9500元,若购进![]() 品牌自行车3辆,
品牌自行车3辆,![]() 品牌自行车2辆,需要进货款4500元.
品牌自行车2辆,需要进货款4500元.
(1)求![]() 、
、![]() 两种品牌自行车每辆进货价分别为多少元;
两种品牌自行车每辆进货价分别为多少元;
(2)今年夏天,车行决定购进![]() 、
、![]() 两种品牌自行车共50辆,在销售过程中,
两种品牌自行车共50辆,在销售过程中,![]() 品牌自行车的利润率为80%,
品牌自行车的利润率为80%,![]() 品牌自行车的利润率为60%,若将所购进的自行车全部销售完毕后其利润不少于29500元,那么此次最少购进多少辆
品牌自行车的利润率为60%,若将所购进的自行车全部销售完毕后其利润不少于29500元,那么此次最少购进多少辆![]() 品牌自行车?
品牌自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为矩形,应添加的条件是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
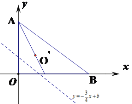
【题目】如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线![]() 对折,点O恰好落在∠OAB的平分线上的O’处,则
对折,点O恰好落在∠OAB的平分线上的O’处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
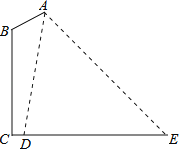
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com