如图.从边长为a的大正方形中剪掉一个边长为b的小正方形.将阴影部分沿虚线剪开.拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是( )A．(a-b)2=a2-2ab+b2B．a(a-b)=a2-abC．(a-b)2=a2-b2D．a2-b2= 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（　　）

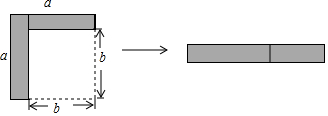
A．

（a-b）²=a²-2ab+b²

B．

a（a-b）=a²-ab

C．

（a-b）²=a²-b²

D．

a²-b²=（a+b）（a-b）

分析利用正方形的面积公式和矩形的面积公式分别表示出阴影部分的面积，然后根据面积相等列出等式即可．

解答解：第一个图形阴影部分的面积是a²-b²，
第二个图形的面积是（a+b）（a-b）．
则a²-b²=（a+b）（a-b）．
故选D．

点评本题考查了平方差公式的几何背景，正确用两种方法表示阴影部分的面积是关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

13．

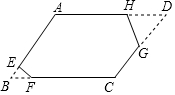如图，?ABCD纸片，∠A=120°，AB=4，BC=5，剪掉两个角后，得到六边形AEFCGH，它的每个内角都是120°，且EF=1，HG=2，则这个六边形的周长为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．计算：|-2|-$\root{3}{8}$=0．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

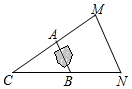如图，A，B两点被池塘隔开，不能直接测量其距离．于是，小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=200m，则A，B间的距离为100m．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

18．计算$\frac{{{{（{x+y}）}^2}-{{（{x-y}）}^2}}}{4xy}$的结果为（　　）

A．

B．

$\frac{1}{2}$

C．

$\frac{1}{4}$

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

8．

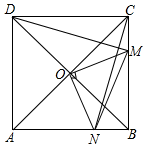如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN²+CM²=MN²；⑤若AB=2，则S_△OMN的最小值是$\frac{1}{2}$，其中正确结论的个数是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．
（1）当⊙O的半径为2时，
①在点P₁（$\frac{1}{2}$，0），P₂（$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}}$），P₃（$\frac{5}{2}$，0）中，⊙O的关联点是P₂，P₃．
②点P在直线y=-x上，若P为⊙O的关联点，求点P的横坐标的取值范围．
（2）⊙C的圆心在x轴上，半径为2，直线y=-x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．