
分析 (1)①根据点P1($\frac{1}{2}$,0),P2($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}}$),P3($\frac{5}{2}$,0),求得OP1=$\frac{1}{2}$,OP2=1,OP3=$\frac{5}{2}$,于是得到结论;②根据定义分析,可得当最小y=-x上的点P到原点的距离在1到3之间时符合题意,设P(x,-x),根据两点间的距离公式即可得到结论;
(2根据已知条件得到A(1,0),B(0,1),如图1,当圆过点A时,得到C(-2,0),如图2,当直线AB与小圆相切时,切点为D,得到C(1-$\sqrt{2}$,0),于是得到结论;如图3,当圆过点A,则AC=1,得到C(2,0),如图4,当圆过点B,连接BC,根据勾股定理得到C(2$\sqrt{2}$,0),于是得到结论.
解答 解:(1)①∵点P1($\frac{1}{2}$,0),P2($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}}$),P3($\frac{5}{2}$,0),
∴OP1=$\frac{1}{2}$,OP2=1,OP3=$\frac{5}{2}$,
∴P1与⊙O的最小距离为$\frac{3}{2}$,P2与⊙O的最小距离为1,OP3与⊙O的最小距离为$\frac{1}{2}$,
∴⊙O,⊙O的关联点是P2,P3;
故答案为:P2,P3;
②根据定义分析,可得当最小y=-x上的点P到原点的距离在1到3之间时符合题意,
∴设P(x,-x),当OP=1时,
由距离公式得,OP=$\sqrt{(x-0)^{2}+(-x-0)^{2}}$=1,
∴x=$±\frac{\sqrt{2}}{2}$,
当OP=3时,OP=$\sqrt{(x-0)^{2}+(-x-0)^{2}}$=3,
解得:x=±$\frac{3\sqrt{2}}{2}$;
∴点P的横坐标的取值范围为:-$\frac{3\sqrt{2}}{2}$≤x≤-$\frac{\sqrt{2}}{2}$,或$\frac{\sqrt{2}}{2}$≤x≤$\frac{3\sqrt{2}}{2}$;
(2)∵直线y=-x+1与x轴、y轴交于点A、B,
∴A(1,0),B(0,1),
如图1,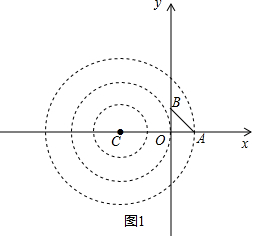
当圆过点A时,此时,CA=3,
∴C(-2,0),
如图2,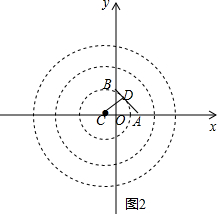
当直线AB与小圆相切时,切点为D,
∴CD=1,
∵直线AB的解析式为y=-x+1,
∴直线AB与x轴的夹角=45°,
∴AC=$\sqrt{2}$,
∴C(1-$\sqrt{2}$,0),
∴圆心C的横坐标的取值范围为:-2≤xC≤1-$\sqrt{2}$;
如图3,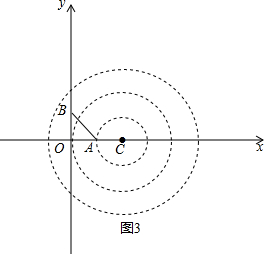
当圆过点A,则AC=1,∴C(2,0),
如图4,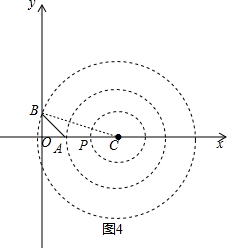
当圆过点B,连接BC,此时,BC=3,
∴OC=$\sqrt{{3}^{2}-1}$=2$\sqrt{2}$,
∴C(2$\sqrt{2}$,0).
∴圆心C的横坐标的取值范围为:2≤xC≤2$\sqrt{2}$;
综上所述;圆心C的横坐标的取值范围为:-2≤xC≤1-$\sqrt{2}$或2≤xC≤2$\sqrt{2}$.
点评 本题考查了一次函数的性质,勾股定理,直线与圆的位置关系,两点间的距离公式,正确的作出图形是解题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
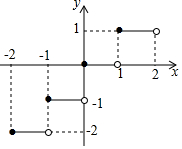 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )| A. | 0或$\sqrt{2}$ | B. | 0或2 | C. | 1或$-\sqrt{2}$ | D. | $\sqrt{2}$或-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
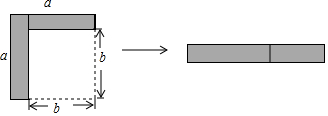
| A. | (a-b)2=a2-2ab+b2 | B. | a(a-b)=a2-ab | C. | (a-b)2=a2-b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 参赛人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com