
| ∞ýº∂ | ≤Œ»¸»À ˝ | ÷–Œª ˝ | ∑Ω≤Ó | ∆Ωæ˘◊÷ ˝ |
| º◊ | 55 | 149 | 191 | 135 |
| ““ | 55 | 151 | 110 | 135 |
| A£Æ | ¢Ÿ¢⁄¢€ | B£Æ | ¢Ÿ¢⁄ | C£Æ | ¢Ÿ¢€ | D£Æ | ¢⁄¢€ |
∑÷Œˆ ∆Ωæ˘ÀÆ∆Ωµƒ≈–∂œ÷˜“™∑÷Œˆ∆Ωæ˘ ˝£ª”≈–„»À ˝µƒ≈–∂œ¥”÷–Œª ˝≤ªÕ¨ø…“‘µ√µΩ£ª≤®∂Ø¥Û–°±»Ωœ∑Ω≤Óµƒ¥Û–°£Æ
Ω‚¥ Ω‚£∫¥”±Ì÷–ø…÷™£¨∆Ωæ˘◊÷ ˝∂º «135£¨¢Ÿ’˝»∑£ª
º◊∞ýµƒ÷–Œª ˝ «149£¨““∞ýµƒ÷–Œª ˝ «151£¨±»º◊µƒ∂ý£¨∂¯∆Ωæ˘ ˝∂º“™Œ™135£¨Àµ√˜““µƒ”≈–„»À ˝∂ý”⁄º◊∞ýµƒ£¨¢⁄’˝»∑£ª
º◊∞ýµƒ∑Ω≤Ó¥Û”⁄““∞ýµƒ£¨”÷Àµ√˜º◊∞ýµƒ≤®∂Ø«Èøˆ¥Û£¨À˘“‘¢€“≤’˝»∑£Æ
π —°A£Æ
µ„∆¿ ±æÂøº≤È¡À∆Ωæ˘ ˝£¨÷–Œª ˝£¨∑Ω≤Óµƒ“‚“£Æ∆Ωæ˘ ˝∆Ωæ˘ ˝±Ì 擪◊È ˝æðµƒ∆Ωæ˘≥Ã∂»£Æ÷–Œª ˝ «Ω´“ª◊È ˝æ𥔖°µΩ¥Û£®ªÚ¥”¥ÛµΩ–°£©÷ÿ–¬≈≈¡–∫Û£¨◊Ó÷–º‰µƒƒ«∏ˆ ˝£®ªÚ◊Ó÷–º‰¡Ω∏ˆ ˝µƒ∆Ωæ˘ ˝£©£ª∑Ω≤Ó «”√¿¥∫‚¡ø“ª◊È ˝æð≤®∂Ø¥Û–°µƒ¡ø£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
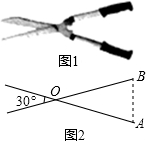 »ÁÕº1 «“ª∞—‘∞¡÷ºÙµ∂£¨∞—À¸≥Ȝی™Õº2£¨∆‰÷–OA=OB£Æ»ÙºÙµ∂’≈ø™µƒΩ«Œ™30°„£¨‘Ú°œA=75∂»£Æ
»ÁÕº1 «“ª∞—‘∞¡÷ºÙµ∂£¨∞—À¸≥Ȝی™Õº2£¨∆‰÷–OA=OB£Æ»ÙºÙµ∂’≈ø™µƒΩ«Œ™30°„£¨‘Ú°œA=75∂»£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 1 | B£Æ | $\frac{1}{2}$ | C£Æ | $\frac{1}{4}$ | D£Æ | 0 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
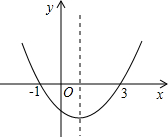 »ÁÕº£¨≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©µƒø™ø⁄œÚ…œ£¨”Îx÷·Ωªµ„µƒ∫·◊¯±Í∑÷±Œ™-1°¢3£¨‘Úœ¬¡–Àµ∑®¥ÌŒÛµƒ «£®°°°°£©
»ÁÕº£¨≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©µƒø™ø⁄œÚ…œ£¨”Îx÷·Ωªµ„µƒ∫·◊¯±Í∑÷±Œ™-1°¢3£¨‘Úœ¬¡–Àµ∑®¥ÌŒÛµƒ «£®°°°°£©| A£Æ | ∂‘≥∆÷· «÷±œþx=1 | B£Æ | ∑Ω≥Ãax2+bx+c=0µƒΩ‚ «x1=-1£¨x2=3 | ||
| C£Æ | µ±x£º1£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û | D£Æ | µ±-1£ºx£º3 ±£¨y£º0 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
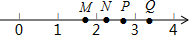 »ÁÕº£¨M£¨N£¨P£¨Q « ˝÷·…œµƒÀƒ∏ˆµ„£¨’‚Àƒ∏ˆµ„÷”◊Ó ∫œ±Ì æ$\sqrt{7}$µƒ «£®°°°°£©
»ÁÕº£¨M£¨N£¨P£¨Q « ˝÷·…œµƒÀƒ∏ˆµ„£¨’‚Àƒ∏ˆµ„÷”◊Ó ∫œ±Ì æ$\sqrt{7}$µƒ «£®°°°°£©| A£Æ | Mµ„ | B£Æ | Nµ„ | C£Æ | Pµ„ | D£Æ | Qµ„ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | $\sqrt{£®-4£©^{2}}$=2 | B£Æ | $\sqrt{2}$°¡$\sqrt{5}$=$\sqrt{10}$ | C£Æ | £®$\sqrt{2}$£©2=4 | D£Æ | $\sqrt{6}$°¬$\sqrt{2}$=3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | y3£ºy1£ºy2 | B£Æ | y1£ºy2£ºy3 | C£Æ | y2£ºy1£ºy3 | D£Æ | y3£ºy2£ºy1 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
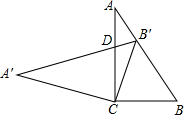 ‘⁄Rt°˜ABC÷–£¨°œC=90°„£¨cosB=0.6£¨∞—’‚∏ˆ÷±Ω«»˝Ω«–Œ»∆∂•µ„C–˝◊™∫Ûµ√µΩRt°˜A'B'C£¨∆‰÷–µ„B'’˝∫√¬‰‘⁄AB…œ£¨A'B'”ÎACœýΩª”⁄µ„D£¨ƒ«√¥B°‰D£∫CD=0.35£Æ
‘⁄Rt°˜ABC÷–£¨°œC=90°„£¨cosB=0.6£¨∞—’‚∏ˆ÷±Ω«»˝Ω«–Œ»∆∂•µ„C–˝◊™∫Ûµ√µΩRt°˜A'B'C£¨∆‰÷–µ„B'’˝∫√¬‰‘⁄AB…œ£¨A'B'”ÎACœýΩª”⁄µ„D£¨ƒ«√¥B°‰D£∫CD=0.35£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com