
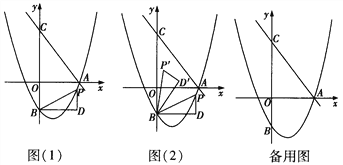
【题目】如图(1),直线![]() 交x轴于点A,交
交x轴于点A,交![]() 轴于点C(0,4),抛物线
轴于点C(0,4),抛物线![]() 过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图(2),将△BDP绕点B 逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
【答案】(1)抛物线的解析式为![]() .(2)
.(2)![]() 或
或![]() .(3)满足条件的点P的坐标为(
.(3)满足条件的点P的坐标为(![]() ,
, ![]() )、(
)、(![]() ,
, ![]() )或(
)或(![]() 、
、![]() ).
).
【解析】(1)先确定出点A的坐标,再用待定系数法求出抛物线解析式;
(2)由△BDP为等腰直角三角形,判断出BD=PD,建立m的方程计算出m,从而求出PD;(3)分点P′落在x轴和y轴两种情况计算即可.
解:(1)∵点C(0,4)在直线y=﹣![]() x+n上,
x+n上,
∴n=4,∴y=﹣![]() x+4,
x+4,
令y=0,∴x=3,∴A(3,0),
∵抛物线y=![]() x2+bx+c经过点A,交y轴于点B(0,﹣2).
x2+bx+c经过点A,交y轴于点B(0,﹣2).
∴c=﹣2,6+3b﹣2=0,
∴b=﹣![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
(2)点P为抛物线上一个动点,设点P的横坐标为m.
∴P(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∴BD=|m|,PD=|![]() m2﹣
m2﹣![]() m﹣2+2|=|
m﹣2+2|=|![]() m2﹣
m2﹣![]() m|,
m|,
∵△BDP为等腰直角三角形,且PD⊥BD,
∴BD=PD,
∴|m|=|![]() m2﹣
m2﹣![]() m|,
m|,
∴m=0(舍),m=![]() ,m=
,m=![]() ,
,
∴PD=![]() 或PD=
或PD=![]() ;
;
(3)∵∠PBP'=∠OAC,OA=3,OC=4,
∴AC=5,
∴sin∠PBP'=![]() ,cos∠PBP'=
,cos∠PBP'=![]() ,
,
①当点P'落在x轴上时,过点D'作D'N⊥x轴,垂足为N,交BD于点M,
∠DBD'=∠ND'P'=∠PBP',
如图1,
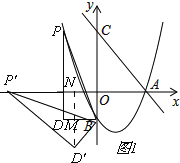
ND'﹣MD'=2,
∴![]() (
(![]() m2﹣
m2﹣![]() m)﹣(﹣
m)﹣(﹣![]() m)=2,
m)=2,
∴m=![]() (舍),或m=﹣
(舍),或m=﹣![]() ,
,
如图2,
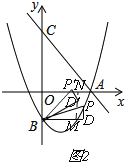
ND'+MD'=2,
∴![]() (
(![]() m2﹣
m2﹣![]() m)+
m)+![]() m=2,
m=2,
∴m=![]() ,或m=﹣
,或m=﹣![]() (舍),
(舍),
∴P(﹣![]() ,
, ![]() )或P(
)或P(![]() ,
, ![]() ),
),
②当点P'落在y轴上时,如图3,
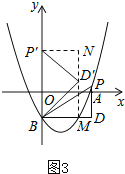
过点D′作D′M⊥x轴,交BD于M,过P′作P′N⊥y轴,
∴∠DBD′=∠ND′P′=∠PBP′,
∵P′N=BM,
∴![]() (
(![]() m2﹣
m2﹣![]() m)=
m)=![]() m,
m,
∴m=![]() ,
,
∴P(![]() ,
, ![]() ).
).
∴P(﹣![]() ,
, ![]() )或P(
)或P(![]() ,
, ![]() )或P(
)或P(![]() ,
, ![]() ).
).
“点睛”此题是二次函数综合题,主要考查了待定系数法求函数解析式,锐角三角函数,等腰直角三角形的性质,解本题的关键是构造直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F在OD上一点,且∠1=∠A. 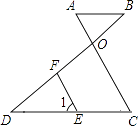
(1)求证:FE∥OC;
(2)若∠DFE=70°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
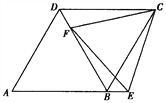
【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面每组数分别是三根小木棒的长度,它们能摆成三角形的是( )
A. 12cm,3cm,6cm B. 8cm,16cm,8cm C. 6cm,6cm,13cm D. 2cm,3cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
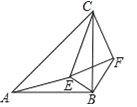
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com