
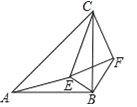
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)首先由△ABC和△CEF均为等腰直角三角形可得AC:BC=CE:CF,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
试题解析:(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴![]() =
=![]() ,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;
,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,∴∠CAE=∠CBF,![]() =
=![]() ,又∵
,又∵![]() =
=![]() ,AE=2,∴
,AE=2,∴![]() =
=![]() ,∴BF=
,∴BF=![]() ,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴
,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴![]() =
=![]() =3,∴EF=
=3,∴EF=![]() ,∵
,∵![]() =6,∴CE=
=6,∴CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
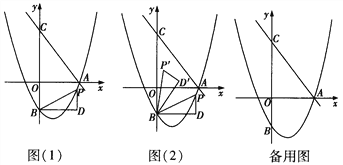
【题目】如图(1),直线![]() 交x轴于点A,交
交x轴于点A,交![]() 轴于点C(0,4),抛物线
轴于点C(0,4),抛物线![]() 过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图(2),将△BDP绕点B 逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com