
【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3)
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 0.24 | |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | |
25<x≤30 | 2 | 0.04 |
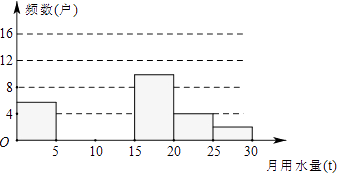
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F在OD上一点,且∠1=∠A. 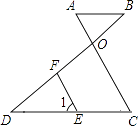
(1)求证:FE∥OC;
(2)若∠DFE=70°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).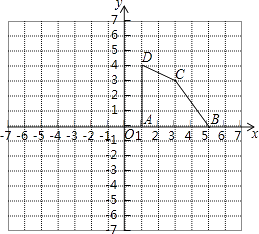
(1)描出A、B、C、D四点的位置,并顺次连接A、B、C、D;
(2)四边形ABCD的面积是;(直接写出结果)
(3)把四边形ABCD向左平移6个单位,再向下平移1个单位得到四边形A′B′C′D′在图中画出四边形A′B′C′D′,并写出A′B′C′D′的坐标.[(1)(3)问的图画在同一坐标系中].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名画家达芬奇验证勾股定理的方法如下:
①在一张长方形的纸板上画两个边长分别为a、b的正方形,并连接BC、FE.
②沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ,请动手做一做.
③将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.
④比较两个多边形ABCDEF和A′B′C′D′E′F′的面积,你能验证勾股定理吗?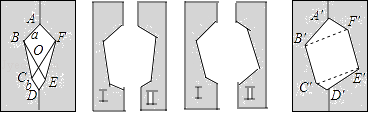
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8. 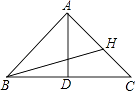
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
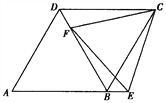
【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
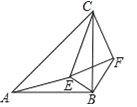
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com