
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8. 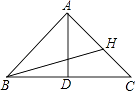
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
【答案】
(1)解:∵AD是BC边上的中线,
∴BD=DC=6.
在△ABD中,BD2+AD2=62+82=102=AB2,
∴△ABD为直角三角形.
∴∠ADB=90°.
∴AD⊥BC.
∵AD⊥BC,BD=DC,
∴AB=AC.
∴△ABC为等腰三角形.
(2)解:∵AH+BH+CH=AC+BH=10+BH,
∴当BH最小时,AH+BH+CH有最小值.
由垂线段的性质可知当BH⊥AC时,BH有最小值.
∴ ![]() BHAC=
BHAC= ![]() BCAD,即
BCAD,即 ![]() ×10BH=
×10BH= ![]() ×12×8,
×12×8,
解得:BH=9.6.
∴AH+BH+CH的最小值=10+9.6=19.6.
【解析】(1)由三角形的中线的定义可知BD=DC=6,然后依据勾股定理的逆定理可证明△ABD为直角三角形,故此AD⊥BC,则AD为BC的垂直平分线,依据线段垂直平分线的性质可知AB=AC;(2)由题意可得到CH+AC=AC=10,故此当BH最小时,AH+BH+CH有最小值,依据垂线段的性质可知当BH⊥AC时,BH有最小值,在△ABC中,依据面积法可求得BH的最小值.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
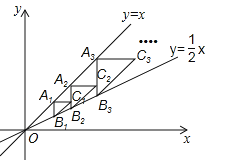
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线![]() 于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和
于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和![]() 于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
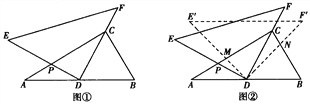
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°.Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过C,且BC=2.
(1)求证:△ADC∽△APD;
(2)求△APD的面积;
(3)如图②,将△DEF绕点D顺时针方向旋转角![]() (0°<
(0°<![]() <60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断
<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否会随着
的值是否会随着![]() 的变化而变化,如果不变,请求出
的变化而变化,如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com