
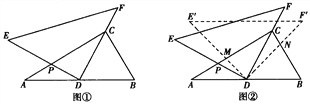
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°.Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过C,且BC=2.
(1)求证:△ADC∽△APD;
(2)求△APD的面积;
(3)如图②,将△DEF绕点D顺时针方向旋转角![]() (0°<
(0°<![]() <60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断
<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否会随着
的值是否会随着![]() 的变化而变化,如果不变,请求出
的变化而变化,如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() 的值不会随着
的值不会随着![]() 的变化而变化,理由见解析.
的变化而变化,理由见解析.
【解析】(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=![]() AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN相似,再根据相似三角形对应边成比例可得![]() =
=![]() 为定值.
为定值.
解:(1)证明:由题意知CD是△ABC中斜边AB上的中线,
∴AD=BD=CD.
∵在△BCD中,BD=CD,且∠B=60°,
∴△BCD为等边三角形.
∴∠BCD=∠BDC=60°,
∴∠ACD=90°-60°=30°,∠ADE=180°-∠BDC-∠EDF=30°,
∴∠ACD=∠ADE=30°,又∵∠A是公共角,
∴△ADC∽△APD.
(2)∵△BCD为等边三角形,∴DC=BC=2.
在Rt△PDC中,∠PCD=30°,∴PD=DCtan30°![]() ,
,
由(1)得∠ADE=30°,又∠PAD=90°-60°=30°,
∴△PAD是等腰三角形,∴AP=PD![]() ,AD=2,
,AD=2,
作PH⊥AD于H,在Rt△PAH中,由∠PAH=30°得![]() ,
,
![]() .
.
(3)![]() 的值不会随着
的值不会随着![]() 的变化而变化.
的变化而变化.
∵∠MPD=∠A+∠ADE=60°,
∴∠MPD=∠BCD=60°.
∵在△MPD和△NCD中,∠MPD=∠NCD=60°,∠PDM=∠CDN= ![]() ,
,
∴△MPD∽△NCD,∴![]() .
.
∵在△APD中,∠A=∠ADE=30°,
∴在等腰△APD中, 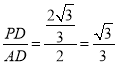 ,
,
∴![]()
“点睛”本题考查了旋转的性质,相似三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质并判断出相似三角形是解题的关键,也是本题的难点.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
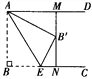
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8. 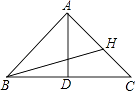
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
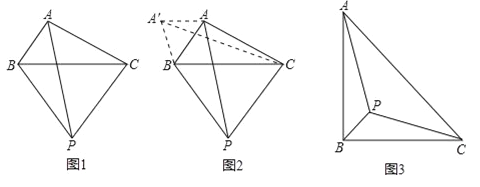
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 . 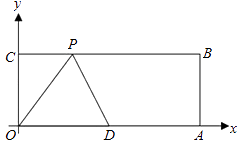
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com