
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
【答案】
(1)55°,35°,90°
(2)解:不变.
由折叠的性质可得:∠BEC=∠B'EC,∠AEN=∠A'EN,
∵∠BEB′=m°,
∴∠AEA'=180°﹣m°,
可得∠BEC=∠B'EC= ![]() ∠BEB′=
∠BEB′= ![]() m°,∠AEN=∠A'EN=
m°,∠AEN=∠A'EN= ![]() ∠AEA'=
∠AEA'= ![]() (180°﹣m°),
(180°﹣m°),
∴∠BEC+∠AEN= ![]() m°+
m°+ ![]() (180°﹣m°)=90°,
(180°﹣m°)=90°,
故∠BEC+∠AEN的值不变 。
(3)解:由折叠的性质可得:∠B'CF=∠B'CE,∠B'CE=∠BCE,
∴∠B'CF=∠B'CE=∠BCE= ![]() ×90°=30°,
×90°=30°,
在Rt△BCE中,
∵∠BEC与∠BCE互余,
∴∠BEC=90°﹣∠BCE=90°﹣30°=60°,
∴∠B'EC=∠BEC=60°,
∴∠AEA'=180°﹣∠BEC﹣∠B'EC=180°﹣60°﹣60°=60°,
∴∠AEN= ![]() ∠AEA'=30°,
∠AEA'=30°,
∴∠ANE=90°﹣∠AEN=90°﹣30°=60°,
∴∠ANE=∠A'NE=60°,
∴∠DNA'=180°﹣∠ANE﹣∠A'NE=180°﹣60°﹣60°=60°
【解析】解:(1)由折叠的性质可得,∠BEC=∠B'EC,∠AEN=∠A'EN,
∵∠BEB′=110°,
∴∠AEA'=180°﹣110°=70°,
∴∠BEC=∠B'EC= ![]() ∠BEB′=55°,∠AEN=∠A'EN=
∠BEB′=55°,∠AEN=∠A'EN= ![]() ∠AEA'=35°.
∠AEA'=35°.
∴∠BEC+∠AEN=55°+35°=90°;
故答案为:55,35,90.
由折叠的性质分别求出∠BEC、∠AEN的度数,然后求出两角之和。
(2) 根据折叠的性质得出∠BEC=∠B'EC,∠AEN=∠A'EN,根据已知用含m的代数式表示出∠AEA',再分别表示出∠BEC,∠AEN,再求和即可得出结论。
(3) 根据折叠的性质求出∠B'CF=∠B'CE=∠BCE=30°,然后在Rt△BCE中,根据直角三角形的性质求出∠BEC的度数,然后再根据折叠的性质及平角的性质求解。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
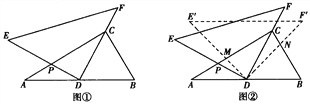
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°.Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过C,且BC=2.
(1)求证:△ADC∽△APD;
(2)求△APD的面积;
(3)如图②,将△DEF绕点D顺时针方向旋转角![]() (0°<
(0°<![]() <60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断
<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否会随着
的值是否会随着![]() 的变化而变化,如果不变,请求出
的变化而变化,如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
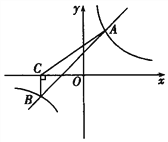
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,4)、B(-4,
的图象交于A(2,4)、B(-4, ![]() )两点.
)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() >
>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
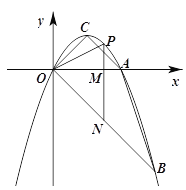
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com