
【题目】如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长. 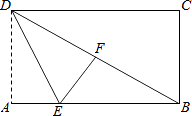
【答案】解:∵四边形ABCD是矩形,∴AD=BC=8, 由折叠性质可知:DF=AD=BC=8,EF=EA,EF⊥BD.
在Rt△BAD中,由勾股定理得:BD= ![]() =
= ![]() =17,
=17,
∵BF=BD﹣DF,
∴BF=17﹣8=9.
设AE=EF=x,则BE=15﹣x.
在Rt△BEF中,由勾股定理可知:EF2+BF2=BE2 ,
即x2+92=(15﹣x)2 ,
解得:x= ![]() .
.
∴AE= ![]() .
.
【解析】由勾股定理可求得BD=17,由翻折的性质可求得BF=9,EF=EA,EF⊥BD,设AE=EF=x,则BE=15﹣x,在Rt△BEF中,由勾股定理列方程求解即可.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为 .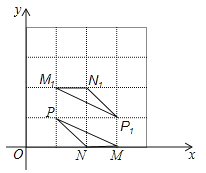
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
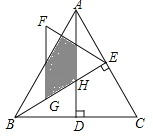
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
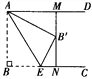
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com