
����Ŀ���Ķ�������ϣ�
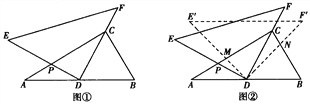
Сΰ��������һ�����⣺��ͼ1���ڡ�ABC�����С�BAC��һ�����Ա仯�Ľǣ��У�AB=2��AC=4����BCΪ����BC���·����ȱߡ�PBC����AP�����ֵ��
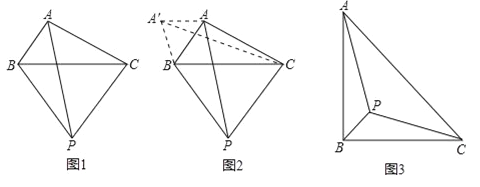
Сΰ������˼���ģ����ñ任�͵ȱ������ν��ߵ�λ��������ϣ����ķ������Ե�BΪ��ת���Ľ���ABP��ʱ����ת60��õ���A��BC������A��A������A����A��C��ʱ������ɽ⣨��ͼ2����
��1������ش�AP�����ֵ�� ��
��2���ο�Сΰͬѧ˼������ķ���������������⣺
��ͼ3������Rt��ABC����AB=4��PΪ��ABC�ڲ�һ�㣬��д����AP+BP+CP����Сֵ���Ľ���˼·��
��ʾ��Ҫ���AP+BP+CP����Сֵ���⣬�ɷ�����Ŀ�������������ѡ�ABP��B����ʱ����ת60���õ���A��BP�䣮
���뻭����ת���ͼ��
����д����AP+BP+CP����Сֵ�Ľ���˼·��������Բ�����
���𰸡���1��6����2������ͼ����������![]() ��˼·��������
��˼·��������
��������
�����������1������ת�õ���A��BC���С�A��BA�ǵȱ������Σ�����A��A��C���㹲��ʱ��A��C=AA��+AC����ɣ�
��2������ת�õ�����PA+PB+PC=P1A1+P1B+PC��ֻ�У�A1��P1��P��C�ĵ㹲��ʱ����P1A+P1B+PC����̣����߶�A1C��̣����ݹ��ɶ��������ɣ�
�����������1���ߡ�ABP��ʱ����ת60��õ���A��BC�����A��BA=60�㣬A��B=AB��AP=A��C
���A��BA�ǵȱ������Σ���A��A=AB=BA��=2���ڡ�AA��C�У�A��C��AA��+AC����AP��6����A��A��C���㹲��ʱ��A��C=AA��+AC����AP=6����AP�����ֵ�ǣ�6��
�ʴ�Ϊ��6��
��2������ת���ͼ����ͼ1��
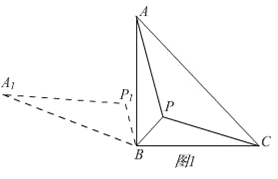
����ͼ2����Rt��ABC�ǵ��������Σ���AB=BC��
��BΪ���ģ�����APB��ʱ����ת60��õ���A1P1B����A1B=AB=BC=4��PA=P1A1��PB=P1B����PA+PB+PC=P1A1+P1B+PC��
�ߵ�A1��P1��P��C�ĵ㹲��ʱ����P1A+P1B+PC����̣����߶�A1C��̣���A1C=PA+PB+PC����A1C���ȼ�Ϊ����
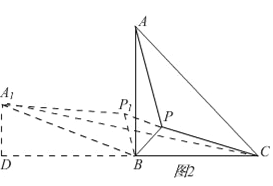
��A1��A1D��CB�ӳ�����D��
�ߡ�A1BA=60�㣨����ת��֪�������A1BD=30�㣮
��A1B=4����A1D=2��BD=![]() ����CD=4+
����CD=4+![]() ��
��
��Rt��A1DC��A1C=![]() =
=![]() =
=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֶ�����������������������ʵ��a��b������a��b=a2-3a+b���磺3��5��32��3��3+5����x��2=6����ʵ��x��ֵ�� ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���BAC=90�㣬AB=AC=2����ACΪһ�ߣ��ڡ�ABC�ⲿ������ֱ��������ACD�����߶�BD�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�dz����Σ���DCE�ǵȱ������Σ�A��0��0����B��4��0����D��0��2������E������꣮ 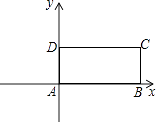
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dz���ͼ�ٰڷţ���Rt��ABC�У���ACB=90�㣬��B=60��.Rt��DEF�У���EDF=90�㣬��E=45�㣩.��DΪAB���е㣬DE��AC�ڵ�P��DF����C����BC=2.
��1����֤����ADC�ס�APD��
��2������APD�������
��3����ͼ�ڣ�����DEF�Ƶ�D˳ʱ�뷽����ת��![]() ��0����
��0����![]() ��60��������ʱ�ĵ���ֱ�����dz�Ϊ��DE��F����DE����AC�ڵ�M��DF����BC�ڵ�N�����ж�
��60��������ʱ�ĵ���ֱ�����dz�Ϊ��DE��F����DE����AC�ڵ�M��DF����BC�ڵ�N�����ж�![]() ��ֵ�Ƿ������
��ֵ�Ƿ������![]() �ı仯���仯��������䣬�����
�ı仯���仯��������䣬�����![]() ��ֵ����֮����˵������.
��ֵ����֮����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ε����ľ�������ԭ�㣬�Ҹ�����x���y��ƽ�У����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������A1 �� A2 �� A3 �� A4 �� ����ʾ����A55�������ǣ� ��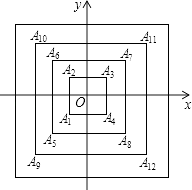
A.��13��13��
B.����13����13��
C.��14��14��
D.����14����14��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
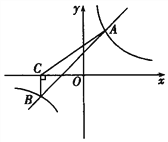
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��2��4����B��-4��
��ͼ����A��2��4����B��-4�� ![]() ������.
������.
��1���ֱ����һ�κ����뷴���������ı���ʽ��
��2������������������ֱ��д������ʽ![]() ��
��![]() �Ľ⼯��
�Ľ⼯��
��3������B��BC��x�ᣬ����ΪC������AC����S��ABC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��DE����B=60�㣬AE��BC������Ϊ��E��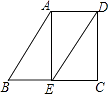
��1�����AED�Ķ�����
��2������EDC����ʲô����ʱ��AE��DC֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com