
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.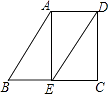
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC证明你的结论.
【答案】
(1)解:∵AE⊥BC,
∴∠AEB=90°,
∵∠B=60°,
∴∠BAE=30°,
又∵AB∥DE,
∴∠AED=∠BAE=30°
(2)解:当∠EDC=30°时,则AE∥DC,理由如下:
∵∠AED=30°,
∴∠AED=∠EDC,
∴AE∥DC(内错角相等,两线平行)
【解析】由AE⊥BC,∠B=60°,得到∠BAE=30°,由平行线AB∥DE的性质,得到∠AED=∠BAE=30°;如果∠AED=∠EDC=30°时,则AE∥DC.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


科目:初中数学 来源: 题型:
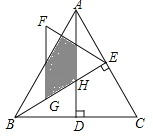
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
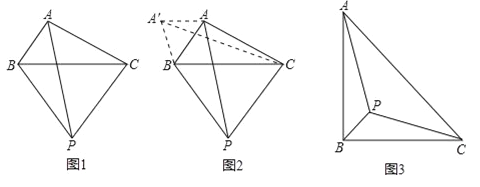
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D为斜边AB的中点,BC=6,CD=5,过点A作AE⊥AD且AE=AD,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区注重城市绿化提高市民生活质量,新建林荫公园计划购买甲、乙两种树苗共800株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去10500元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠A=∠F,∠C=∠D,按图填空,并在括号内注明理由.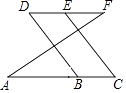
∵∠A=∠F()
∴∥()
∴∠D=∠ABD()
又∵∠D=∠C()
∴∠C=∠ABD()
∴∥()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com