
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 . 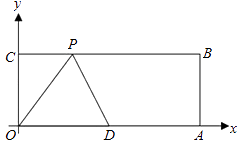
【答案】(2,4)或(3,4)或(8,4)
【解析】解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况: (i)如答图①所示,PD=OD=5,点P在点D的左侧.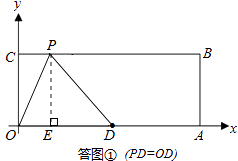
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE= ![]() =
= ![]() =3,
=3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(ii)如答图②所示,OP=OD=5.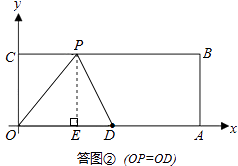
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE= ![]() =
= ![]() =3,
=3,
∴此时点P坐标为(3,4);
(iii)如答图③所示,PD=OD=5,点P在点D的右侧.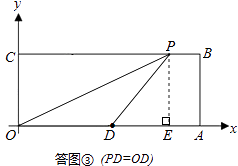
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE= ![]() =
= ![]() =3,
=3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
所以答案是:(2,4)或(3,4)或(8,4).
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
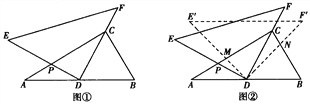
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°.Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过C,且BC=2.
(1)求证:△ADC∽△APD;
(2)求△APD的面积;
(3)如图②,将△DEF绕点D顺时针方向旋转角![]() (0°<
(0°<![]() <60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断
<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否会随着
的值是否会随着![]() 的变化而变化,如果不变,请求出
的变化而变化,如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
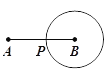
【题目】如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
A. 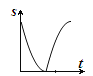 B.
B. 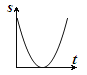 C.
C. 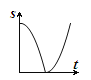 D.
D. 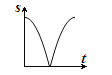
查看答案和解析>>
科目:初中数学 来源: 题型:
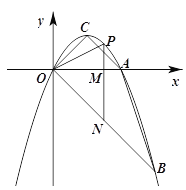
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 以下调查中适合作抽样调查的有( ).
① 了解全班同学期末考试的数学成绩情况; ② 了解夏季冷饮市场上冰淇淋的质量情况;③ 学校为抗击“非典”,需了解全校师生的体温; ④ 了解《课课练》在全省七年级学生中受欢迎的程序.
A. 1个 B. 2个 C. 3个 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个. 求:
(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com