
| A. | 1005 | B. | 1006 | C. | 2012 | D. | 2010 |
分析 根据f(a+b)=f(a)+f(b),可得f(a+a)=f(a)+f(a)=2f(a),即f(2a)=2f(a),据此可得f(2)=2f(1),f(4)=2f(2),f(6)=2f(3),f(8)=2f(4),…,据此求出$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(2)}$+$\frac{f(6)}{f(3)}$+…+$\frac{f(2012)}{f(1006)}$的值是多少即可.
解答 解:因为f(a+b)=f(a)+f(b),
所以f(a+a)=f(a)+f(a)=2f(a),
即f(2a)=2f(a),
所以f(2)=2f(1),f(4)=2f(2),f(6)=2f(3),f(8)=2f(4),…,
因此$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(2)}$+$\frac{f(6)}{f(3)}$+…+$\frac{f(2012)}{f(1006)}$
=$\underset{\underbrace{2+2+…+2}}{1006个2}$
=2012
故选:C.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是根据f(a+b)=f(a)+f(b),判断出:f(2a)=2f(a).


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
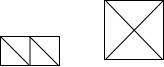 如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
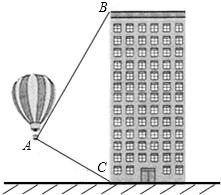 小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
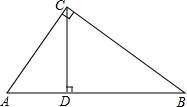 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
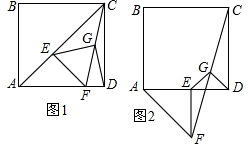
 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com