【题目】求1+2+22+23…+22012的值，可令S=1+2+22+23+…+22012，则2S=2+22+23+24+…+22013，因此2S﹣S=22013﹣1，仿照以上推理，计算出1+5+52+53+…+52017的值为（ ）
A. 52017﹣1 B. 52018﹣1 C. 
D. 
科目：初中数学 来源： 题型：
【题目】（1）阅读下面材料：
点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为|AB|．
当A，B两点中有一点在原点时，不妨设点A在原点，如图（1），|AB|=|OB|=|b|=|a﹣b|；当A，B两点都不在原点时，
①如图（2），点A，B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；
②如图（3），点A，B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；
③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=|a﹣b|；
综上，数轴上A，B两点之间的距离|AB|=|a﹣b|．
（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是 ，数轴上表示﹣2和﹣5的两点之间的距离是 ，数轴上表示1和﹣3的两点之间的距离是 ；
②数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|=2，那么x为 ；
③当代数式|x+1|+|x﹣2|取最小值时，相应的x的取值范围是 ．
④解方程|x+1|+|x﹣2|=5．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知A（
，y1），B（2，y2）为反比例函数y=
图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
A.（，0） B.（1，0） C.（
，0） D.（
，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为奖励学习之星，准备在某商店购买A、B两种文具作为奖品，已知一件A种文具的价格比一件B种文具的价格便宜5元，且用600元买A种文具的件数是用400元买B种文具的件数的2倍．
（1）求一件A种文具的价格；
（2）根据需要，该校准备在该商店购买A、B两种文具共150件．
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式；
②若购买A种文具的件数不多于B种文具件数的2倍，且计划经费不超过2750元，求有几种购买方案，并找出经费最少的方案，及最少需要多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，对角线AC平分∠DAB，∠ABD=52°，∠ABC=116°，∠ACB=α°，则∠BDC的度数为（ ）
A. α B. 
C. 90﹣α D. 90﹣
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A的坐标为（﹣
，0），点B的坐标为（0，3）．
（1）求过A，B两点直线的函数表达式；
（2）过B点作直线BP与x轴交于点P，且使OP=2OA，求△ABP的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
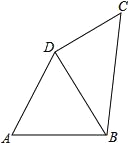
【题目】如图，在四边形ABCD中，AB=AD=8，∠A=60°，∠ADC=150°，四边形ABCD的周长为32．
（1）求∠BDC的度数；
（2）四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）已知：点A和点B（如图1），根据条件画图（用三角板和量角器）：
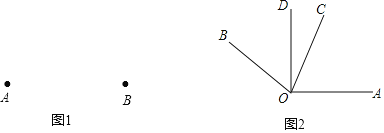
①画射线BA；
②画∠ABC＝90°，使得点C在线段AB上方且AB＝BC；
③连接AC，画出∠ABC的角平分线BD，交AC于D．通过观察、度量、猜想获得线段BD、AC的关系．
（2）已知：如图2，∠AOB＝150，OC平分∠AOB，AO⊥DO，求∠COD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．
（1）求证：BE=CD；
（2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
