
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
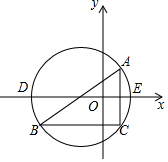 如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).
如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
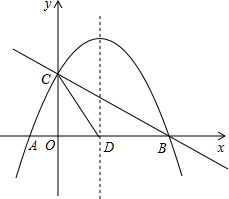 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
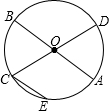 如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.
如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
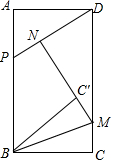 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com