解:(1)∵tan63°=cot27°,tan27°<tan63°,
∴tan27°<cot27°.
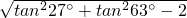
=

=
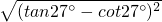
=|tan27°-cot27°|
=cot27°-tan27°;
sin
2l°+sin
22°+…+sin
288°+sin
289°
=(sin
2l°+sin
289°)+(sin
22°+sin
288°)+…+(sin
244°+sin
246°)+sin
245°
=1+1+…+1+

=44

.
故答案为cot27°-tan27°;44

.
分析:(1)先根据互为余角的三角函数关系式,将被开方数变形为(tan27°-cot27°)
2,再由二次根式的性质

=|a|及锐角三角函数的增减性得出结果;
(2)由sin
2α+cos
2α=1及sinα=cos(90°-α),可知sin
2l°+sin
289°=sin
22°+sin
288°=…=sin
244°+sin
246°=1,先将原式分成44组,每一组的值都是1,计算出它们的和再加上sin
245°,即可得出结果.
点评:本题主要考查了互为余角的三角函数关系式,完全平方公式,二次根式的性质,锐角三角函数的增减性
及特殊角的三角函数值,综合性较强,难度中等.解第(1)题的关键是将被开方数变形为一个完全平方式;解第(2)题的关键是将式子恰当分组.
用到的知识点:
互为余角的三角函数关系式:tanα=cot(90°-α);tanα•cotα=1;sin
2α+cos
2α=1;sinα=cos(90°-α).
完全平方公式:a
2-2ab+b
2=(a-b)
2;
二次根式的性质:

=|a|;
锐角三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);
sin45°=

.

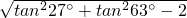 =______;
=______;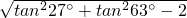

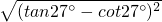

 .
. .
. =|a|及锐角三角函数的增减性得出结果;
=|a|及锐角三角函数的增减性得出结果; =|a|;
=|a|; .
. 

 如图1,由直角三角形边角关系,可将三角形面积公式变形,
如图1,由直角三角形边角关系,可将三角形面积公式变形,