
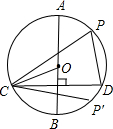
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD. 上一点(不与C,D重合),∠CPD与∠COB有何大小关系?试说明理由;
上一点(不与C,D重合),∠CPD与∠COB有何大小关系?试说明理由; 上(不与C,D重合)时,∠CP'D与∠COB又有什么数量关系?为什么?
上(不与C,D重合)时,∠CP'D与∠COB又有什么数量关系?为什么?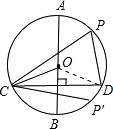 (1)∠CPD=∠COB.…(1分)
(1)∠CPD=∠COB.…(1分) =
= ,…(3分)
,…(3分) ∠COD.…(4分)
∠COD.…(4分) ∠COD,
∠COD, ∠COD,∠CP'D=
∠COD,∠CP'D= (360°-∠COD)=180°-
(360°-∠COD)=180°- ∠COD,
∠COD,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com