
 ��
��

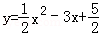 ����������������������������4��
����������������������������4��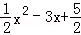 ��������ͼ��ʾ��
��������ͼ��ʾ��
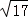 ����λ��2����λ������ƽ��
����λ��2����λ������ƽ�� ��1����λ����ʹ����C��D��M��NΪ������ı�����ƽ���ı��Σ�
��1����λ����ʹ����C��D��M��NΪ������ı�����ƽ���ı��Σ� 


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2011-2012�걱����������ѧ���꼶��ѧ�����в�����ѧ�� ���ͣ������
��֪������ ��
��
����1����1���� ��
�� �������������
������������� �ṫ��������ꣻ
�ṫ��������ꣻ
��С��2����2���� ���ҵ�
���ҵ�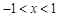 ʱ����������
ʱ���������� ������ֻ��һ�������㣬��
������ֻ��һ�������㣬�� ��ȡֵ��Χ��
��ȡֵ��Χ��
����3����3���� ����
���� ʱ����Ӧ��
ʱ����Ӧ�� ��
�� ʱ����Ӧ��
ʱ����Ӧ�� �����жϵ�
�����жϵ� ʱ����������
ʱ���������� ���Ƿ��й����㣿���У��м�����֤����Ľ��ۣ���û�У��������ɣ�
���Ƿ��й����㣿���У��м�����֤����Ľ��ۣ���û�У��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012�걱������·��ѧ���꼶��һѧ�����в�����ѧ�� ���ͣ������
��֪������ ����С��1��<1>�������߶���M�����ꣻ
����С��1��<1>�������߶���M�����ꣻ
��С��2����<2>����������x��Ľ���ֱ�Ϊ��A��B����A�ڵ�B����ߣ�����y�ύ�ڵ�C����NΪ�߶�BM�ϵ�һ�㣬����N��x��Ĵ��ߣ�����Ϊ��Q������N���߶�BM���˶�ʱ����N�����B����M�غϣ�����NQ�ij�Ϊt���ı���NQAC�����ΪS����S��t֮��ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��С��3����<3>�ڶԳ����Ҳ�����������Ƿ���ڵ�P��ʹ��PACΪֱ��������?�����ڣ�������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�챱����ƽ���п�ģ����ѧ��� ���ͣ������
��֪������ ��
��
��С��1����n="-1," ����������� ��Ľ������ꣻ
��Ľ������ꣻ
��С��2���� ʱ����������
ʱ���������� ������ֻ��һ�������㣬��n��ȡֵ��Χ��
������ֻ��һ�������㣬��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�챱��ͨ�����п�ģ����ѧ�� ���ͣ������
��֪������ ��
��
��С��1���������߶���M�����ꣻ
��С��2������������x��Ľ���ֱ�Ϊ��A��B����A�ڵ�B����ߣ�����y�ύ�ڵ�C����NΪ�߶�BM�ϵ�һ�㣬����N��x��Ĵ��ߣ�����Ϊ��Q������N���߶�BM���˶�ʱ����N�����B����M�غϣ�����NQ�ij�Ϊt���ı���NQAC�����ΪS����S��t֮��ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��С��3���ڶԳ����Ҳ�����������Ƿ���ڵ�P��ʹ��PACΪֱ��������?�����ڣ�������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�콭��ʡ��Ӧ�ؾ��꼶�����ľ���Ӧ�Բ�����ѧ������������ ���ͣ������
��֪������ ��
��
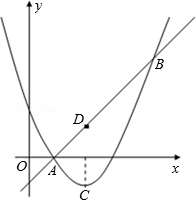
��С��1����˵��������mΪ��ʵ��������������x������������ͬ�Ľ��㣻
��С��2����ͼ���������ߵĶԳ���Ϊֱ��x=3ʱ�������ߵĶ���Ϊ��C��ֱ��y=x��1�������߽���A��B���㣬�������ĶԳ��ύ�ڵ�D��
�����������Ƿ����һ��Pʹ���ı���ACPD�������Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��ƽ��ֱ��CD����ֱ��AB�ڵ�M�����������ڵ�N��ͨ��������ƽ����ʹ����C��D��M��NΪ������ı�����ƽ���ı��Σ���ֱ��д��ƽ�Ƶķ�������Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com