
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)当![]() 为何值时,方程有两个不相等的实数根?
为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求![]() 的值.
的值.
【答案】(1)当m>﹣![]() 时,方程有两个不相等的实数根;(2)m的值为﹣4.
时,方程有两个不相等的实数根;(2)m的值为﹣4.
【解析】
试题分析:(1)根据方程的系数结合根的判别式,即可得出△=4m+17>0,解之即可得出结论;
(2)设方程的两根分别为a、b,根据根与系数的关系结合菱形的性质,即可得出关于m的一元二次方程,解之即可得出m的值,再根据a+b=﹣2m﹣1>0,即可确定m的值.
试题解析:(1)∵方程x2+(2m+1)x+m2﹣4=0有两个不相等的实数根,
∴△=(2m+1)2﹣4(m2﹣4)=4m+17>0,
解得:m>﹣![]() .
.
∴当m>﹣![]() 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
(2)设方程的两根分别为a、b,
根据题意得:a+b=﹣2m﹣1,ab=m2﹣4.
∵2a、2b为边长为5的菱形的两条对角线的长,
∴a2+b2=(a+b)2﹣2ab=(﹣2m﹣1)2﹣2(m2﹣4)=2m2+4m+9=52=25,
解得:m=﹣4或m=2.
∵a>0,b>0,
∴a+b=﹣2m﹣1>0,
∴m=﹣4.
若边长为5的菱形的两条对角线的长分别为方程两根的2倍,则m的值为﹣4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过点P作PF∥AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)以P、E、F为顶点的三角形与△EDG能否相似?如果能相似,请求出.BP的长,如果不能,请说明理由.

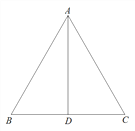
(备用图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com