练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
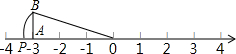
    19．在数轴上画出表示-$\sqrt{10}$的点．（数轴画在横线上）

    分析 因为10=9+1，则首先作出以1和3为直角边的直角三角形，则其斜边的长即是$\sqrt{10}$．再以原点为圆心，以$\sqrt{10}$为半径画弧，和数轴的负半轴交于一点P，则点P即是要作的点．

    解答 解：如图：OA=3，AB=1，AB⊥OA，由勾股定理得：OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
    以O为圆心，OB为半径画弧交数轴的负半轴于点P，点P即表示-$\sqrt{10}$的点．

    故答案为

    点评 此题考查的知识点是勾股定理，实数与数轴，关键是能够正确运用数轴上的点来表示一个无理数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．解方程组：$\left\{\begin{array}{l}{5x+y+z=6}\\{x+5y+z=-2}\\{x+y+5z=10}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．将Rt△ABO放置在如图所示的平面直角坐标系中，∠A=90°，∠AOB=60°，OB=2$\sqrt{3}$．斜边OB在x轴的正半轴上，点A在第一象限，∠AOB的平分线OC交AB于C．求：
    （1）点A、点C的坐标；
    （2）在x轴上是否存在一点Q，使得以点C、O、Q为顶点的三角形是等腰三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；
    （3）过点C作△OCB的高CP，这时△BCP固定，△COP沿x轴正半轴方向以每秒1个单位的速度平移，设运动的总时间为t（0≤t≤2$\sqrt{3}$），△COP与△BCP的重叠部分面积为S，求S与t的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

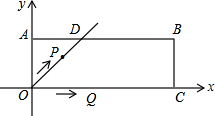    7．在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．
    （1）当点P移动到点D时，求出此时t的值；
    （2）当t为何值时，△PQB为直角三角形；
    （3）已知过O、P、Q三点的抛物线解析式为y=$\frac{1}{t}$（x-t）2+t（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

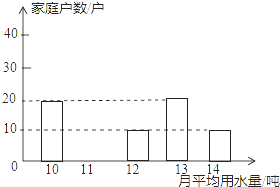    14．自来水公司对某社区600户居民家庭的用水情况做了一次调查．调查小组随机抽查了其中的100户家庭一年的月平均用电量（单位：吨），并将调查结果制成了如图所示的条形统计图．
    （1）请将条形统计图补充完整；
    （2）求这100个样本数据的平均数，众数和中位数；
    （3）根据样本数据，估计该社区600户家庭中月平均用水量不超过12吨的约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．在△ABC中，AB=6，AC=9，则第三边BC的值可以是3＜BC＜15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．一只不透明的口袋中装有10个小球，它们只有颜色不同，其中红球4个，黄球6个，从中随机摸出一球，是红球的概率为：$\frac{2}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．将一个圆分割成三个扇形，使它们圆心角度数比为2：3：4，则这3个圆心角中度数最大的为160°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．某种感冒病毒的直径是0.000000712米，用科学记数法表示为7.12×10-7米．

    查看答案和解析>>

    同步练习册答案