
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
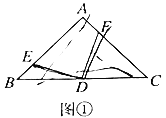
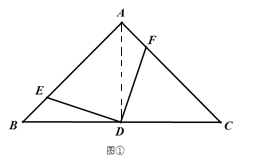
(1)观察猜想:如图①,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() 于点
于点![]() ,则线段
,则线段![]() 与
与![]() 的数量关系是_______;(不说明理由)
的数量关系是_______;(不说明理由)
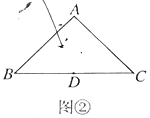
(2)类比探究:若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() 于点
于点![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,在图②中画出符合题意的图形,并说明理由;
的数量关系,在图②中画出符合题意的图形,并说明理由;
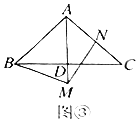
(3)解决问题:如图③,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.(直接写出结果,不说明理由.)
的长.(直接写出结果,不说明理由.)
【答案】(1)BE=AF;(2)BE=AF,理由见解析;(3)![]() .
.
【解析】
(1)连接AD,根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△BDE≌△ADF(ASA),再根据全等三角形的性质即可证出BE=AF;
(2)连接AD,根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△EDB≌△FDA(ASA),再根据全等三角形的性质即可得出BE=AF;
(3)过点M作MG∥BC,交AB的延长线于点G,同理证明△BMG≌△NMA,得到AN=GB=1,再根据等腰直角三角形求出AG的长,即可求解.
(1)证明:连接AD,如图①所示.
∵∠A=90°,AB=AC,
∴△ABC为等腰直角三角形,∠EBD=45°.
∵点D为BC的中点,
∴AD=![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,
∴∠BDE=∠ADF.
在△BDE和△ADF中,
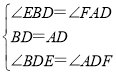 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.
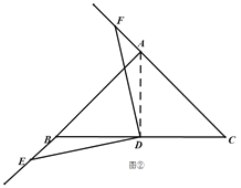
(2)BE=AF
理由:如图②,连结AD,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=![]() (180°-∠BAC)=
(180°-∠BAC)=![]() (180°-90°)=45°
(180°-90°)=45°
∵BD=AD,AB=AC,
∴AD⊥BC,
∴∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×90°=45°,
×90°=45°,
∴∠BAD=∠ABC,
∴AD=BD
又∠CAD=∠ABC=45°,
∴∠DAF=∠DBE=135°
∵DE⊥DF,
∴∠BDE+∠BDF=90°
又AD⊥BC,
∴∠ADF+∠BDF=90°,
∴∠BDE=∠ADF
在△BDE和△ADF中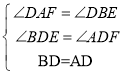 ,
,
∴△BDE≌△ADF,
∴BE=AF
(3)如图③,过点M作MG∥BC,交AB的延长线于点G,
∵DA⊥BC,
∴AM⊥GM,
故△AMG为等腰直角三角形
∴GM=AM=2,故AG=2![]()
∵![]()
同(1)理可得△BMG≌△NMA,
∴AN=GB=1,
∴![]() =AG-BG=AG-AN=
=AG-BG=AG-AN=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
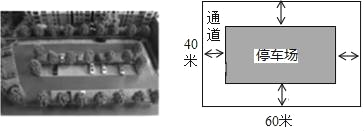
【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解析:
由分母为![]() ,可设
,可设![]()
则![]()
![]() 对应任意x,上述等式均成立,
对应任意x,上述等式均成立,![]() ,
,![]() ,
,![]() .
.
![]() .
.
这样,分式![]() 被拆分成了一个整式
被拆分成了一个整式![]() 与一个分式
与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)当![]() 时,直接写出
时,直接写出![]() ________,
________,![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的函数y=(5m-3)x2-n+(m+n).
(1)当m,n为何值时,函数是一次函数?
(2)当m,n为何值时,函数是正比例函数?
(3)当m,n为何值时,函数是反比例函数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com