
【题目】问题情境:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 于点D.可知:
于点D.可知:![]() 不需要证明
不需要证明![]() ;
;
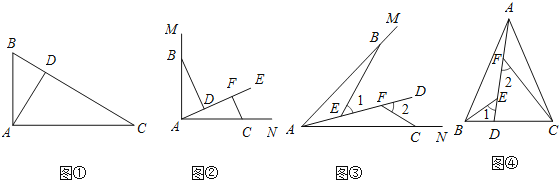
![]() 特例探究:如图
特例探究:如图![]() ,
,![]() ,射线AE在这个角的内部,点B、C在
,射线AE在这个角的内部,点B、C在![]() 的边AM、AN上,且
的边AM、AN上,且![]() ,
,![]() 于点F,
于点F,![]() 于点
于点![]() 证明:
证明:![]() ≌
≌![]() ;
;
![]() 归纳证明:如图
归纳证明:如图![]() ,点B,C在
,点B,C在![]() 的边AM、AN上,点E,F在
的边AM、AN上,点E,F在![]() 内部的射线AD上,
内部的射线AD上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角
的外角![]() 已知
已知![]() ,
,![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 拓展应用:如图
拓展应用:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点D在边BC上,
点D在边BC上,![]() ,点E、F在线段AD上,
,点E、F在线段AD上,![]() 若
若![]() 的面积为24,则
的面积为24,则![]() 与
与![]() 的面积之和为______
的面积之和为______![]() 直接写出结果
直接写出结果![]()
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为增加环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收 集的数据绘制了如图所示的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)本次抽样调查了多少个家庭?
(2)将图①中的频数分布直方图补充完整;
(3)求用车时间在 1 小时~1.5 小时的部分对应的扇 形圆心角的度数;
(4)若该社区有车家庭有 1 600 个,请你估计该社区用车时间不超过 1.5 小时的约有多少个家庭.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交OG于点H.
(1)求证:∠DAE=∠DCG.
(2)求线段HE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
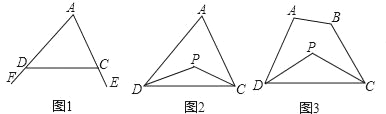
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里”的交通接驳问题,某市投放了大量公租自行车使用,到2014年底,全市已有公租自行车25000辆,租赁点600个,预计到2016年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
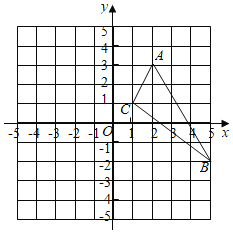
【题目】已知如图,在![]() 中,三个顶点的坐标分别为
中,三个顶点的坐标分别为![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,其 中点
,其 中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]()
![]() 直接写出平移后的
直接写出平移后的![]() 的顶点坐标:
的顶点坐标:
![]()
![]()
![]()
![]() 在坐标系中画出平移后的
在坐标系中画出平移后的![]()
![]() 求出
求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: 用 2 辆![]() 型车和 1 辆
型车和 1 辆![]() 型车载满货物一次可运货 10 吨; 用 1 辆
型车载满货物一次可运货 10 吨; 用 1 辆![]() 型车和 2 辆
型车和 2 辆![]() 型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
(1) 1 辆![]() 型车和 1 辆
型车和 1 辆![]() 型车载满货物一次可分别运货多少吨?
型车载满货物一次可分别运货多少吨?
(2) 某物流公司现有货物若干吨要运输, 计划同时租用![]() 型车 6 辆,
型车 6 辆,![]() 型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,cos∠ABC= ![]() ,sin∠ACB=
,sin∠ACB= ![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 .
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com