
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(黑龙江龙东卷)数学(解析版) 题型:填空题
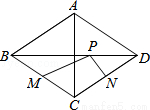
如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:解答题
在△ABC中,AB=AC=5,BC=6,以AC为一边作正方形ACDE,过点D作DF⊥BC交直线BC于点F,连接AF,请你画出图形,直接写出AF的长,并画出体现解法的辅助线.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:解答题
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:填空题
如图,矩形ABCD中,AD= ,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB= .
,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB= .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:选择题
对坐标平面内不同两点A(x1,y1)、B(x2,y2),用|AB|表示A、B两点间的距离(即线段AB的长度),用‖AB‖表示A、B两点间的格距,定义A、B两点间的格距为‖AB‖=|x1-x2|+|y1-y2|,则|AB|与‖AB‖的大小关系为( )
A.|AB|≥‖AB‖ B.|AB|>‖AB‖ C.|AB|≤‖AB‖ D.|AB|<‖AB‖
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:选择题
反比例函数y1= 和正比例函数y2=mx的图象如图,根据图象可以得到满足y1<y2的x的取值范围是( )
和正比例函数y2=mx的图象如图,根据图象可以得到满足y1<y2的x的取值范围是( )

A.x>1 B.-<x<1或x<-1 C.-1<x<0或x>1 D.x>2或x<1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com