
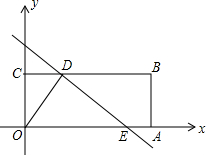
 如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=- +b交折线OAB于点E.
+b交折线OAB于点E.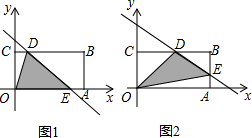 解:(1)若直线经过点A(6,0)时,则b=3,
解:(1)若直线经过点A(6,0)时,则b=3, OE•OC=
OE•OC= ×2b×2=2b;
×2b×2=2b; ×2×(2b-4)-
×2×(2b-4)- ×(10-2b)×(5-b)-
×(10-2b)×(5-b)- ×6×(b-3)=5b-b2,
×6×(b-3)=5b-b2,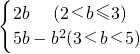 ;
; (2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积.
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积. ,DH=2,
,DH=2, ,
, ,DH=2,设菱形DNEM的边长为a,由勾股定理知:a2=(4-a)2+22,可求得a的值,继而求得重叠部分的面积.
,DH=2,设菱形DNEM的边长为a,由勾股定理知:a2=(4-a)2+22,可求得a的值,继而求得重叠部分的面积.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( )
如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( )A、2
| ||
B、
| ||
| C、4 | ||
| D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 端点B、C不重合),过点D作直线y=-
端点B、C不重合),过点D作直线y=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
(2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
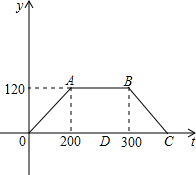 小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s=v0t+
小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s=v0t+| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点
如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com