
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:x1,x2,x3,称为数列x1,x2,x3.计算![]()
![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的价值。例如,对于数列2,1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的价值。例如,对于数列2,1,3,因为|2|=2,![]() ,
,![]() ,所以数列2,1,3的价值为
,所以数列2,1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值。如数列1,2,3的价值为![]() ;数列3,1,2的价值为1;….经过研究,小丁发现,对于“2,1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,1,2的价值为1;….经过研究,小丁发现,对于“2,1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列4,3,2的价值为___;
(2)将“4,3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为___,取得价值最小值的数列为___(写出一个即可);
(3)将2,9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列。若这些数列的价值的最小值为1,则a的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.

利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|=
④若x表示一个有理数,且|x-2|+|x+4|=8,则有理数x的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
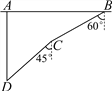
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.
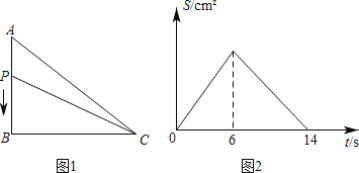
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小正方形卡片(如图1)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子的底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分的周长和是( )
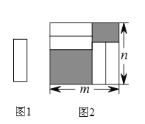
A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.
请用上面的知识解答下面的问题:
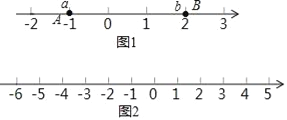
如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.
(1)请你在数轴上表示出A.B.C三点的位置:
(2)点C到点人的距离CA= cm;若数轴上有一点D,且AD=4,则点D表示的数为 ;
(3)若将点A向右移动xcm,则移动后的点表示的数为 ;(用代数式表示)
(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,
试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
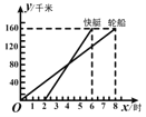
【题目】如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t(时)变化的图象,根据图象回答下列问题
(1)轮船的行驶速度是___________km/h;
(2)当2≤t≤6时,求快艇行驶过程y与t的函数关系式;
(3)当快艇与乙港相距40 km时,快艇和轮船相距___________km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com