
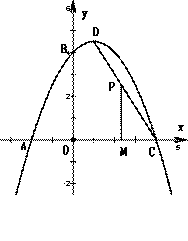
如图,一抛物线经过点A、B、C,点 A(−2,0),点B(0,4),点C(4,0),该抛物线的顶点为D.
(1)求该抛物线的解析式及顶点D坐标;
(2) 如图,若P为线段CD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAB的面积的最大值和此时点P的坐标;
(3)过抛物线顶点D,作DE⊥x轴于E点,F(m,0)是x轴上一动点,若以BF为直径的圆与线段DE有公共点,求m的取值范围.
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
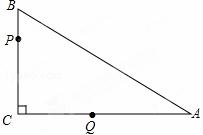
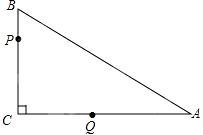
如图,在△ABC中,∠C=90°,BC=3,AB=5.点P从点B出发,以每秒1个单位长度沿B→C→A→B的方向运动;点Q从点C出发,以每秒 2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
(1)当t= 时,点P与点Q相遇;
(2)在点P从点B到点C的运动过程中,当ι为何值时,△PCQ为等腰三角形?
(3)在点Q从点B返回点A的运动过程中,设△PCQ的面积为s平方单位.求s与ι之间的函数关系式;
|
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f (x,y) = (x+2, y).② g(x,y) = (−x , −y), 例如按照以上变换有: f (1,1) = (3, 1); g( f (1,1) ) = g (3 , 1) = (−3,−1).如果有数a、b, 使得f ( g(a,b )) = (b,a ),则g( f (a+b , a−b) ) = .
查看答案和解析>>
科目:初中数学 来源: 题型:
据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图①)、扇形图(图②).
(1)图2中所缺少的百分数是____________;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是____ _ __(填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是_____________;
 (4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有___________名.
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有___________名.
 |
图 ① 图 ②
查看答案和解析>>
科目:初中数学 来源: 题型:
下列二次函数中,图象以x = −1为对称轴,且经过点(0,2)的是 ……………( )
A.y = (x − 1)2 − 1 B.y = (x + 1)2 − 1
C.y = (x − 1)2 + 1 D.y = (x + 1)2 + 1
查看答案和解析>>
科目:初中数学 来源: 题型:
一汽车销售公司销售某品牌型号的汽车,已知每辆汽车的进货价为25万元.经市场调查发现:当每辆汽车的销售价为29万元时,平均每周能售出8辆;而当销售价每降低0.5万元时,平均每周能多售出4辆.如果假设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润 = 销售价 - 进货价 )
(1)求y与x之间的函数关系式,在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的销售价定为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
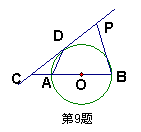
如图所示,直线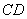 与线段
与线段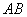 为直径的圆相切于点
为直径的圆相切于点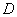 ,并交
,并交 的延长线于点
的延长线于点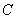 ,且
,且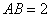 ,
,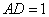 ,
,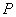 点在切线
点在切线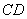 上移动.当
上移动.当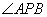 的度数最大时,则
的度数最大时,则 的度数为 ( )
的度数为 ( )
A.  ° B.
° B. 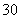 ° C.
° C. 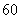 ° D.
° D. 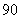 °
°
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com