
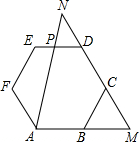
 如图所示,正六边形ABCDEF中,P是ED上一点,直线DC与AP、AB延长线分别相交于点N、M.若三角形AMN和正六边形ABCDEF的面积相等,EP:PD=1:2.
如图所示,正六边形ABCDEF中,P是ED上一点,直线DC与AP、AB延长线分别相交于点N、M.若三角形AMN和正六边形ABCDEF的面积相等,EP:PD=1:2. 分析 连接AE,过点F做FG⊥AE于点G,设正六边形ABCDEF的边长为a,△NPD的高为h,利用a表示出六边形的面积,再用a表示出h的值,根据△NPD∽△NAM可得出PD的长,进而可得出PE的长,由此可得出结论.
解答 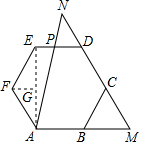 解:连接AE,过点F做FG⊥AE于点G,设正六边形ABCDEF的边长为a,△NPD的高为h,
解:连接AE,过点F做FG⊥AE于点G,设正六边形ABCDEF的边长为a,△NPD的高为h,
∵AE=2EG=2EF•cos∠AEF=2a×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$a,
S六边形ABCD=6×$\frac{1}{2}$a×$\frac{\sqrt{3}a}{2}$=$\frac{3\sqrt{3}{a}^{2}}{3}$.
∵∠ABC=∠BCD=120°,
∴∠CBM=∠BCM=60°,
∴△BMC是等边三角形,
∴BM=a.
∵△AMN和正六边形ABCDEF的面积相等,
∴S△AMN=$\frac{1}{2}$AM×(AE+h)=$\frac{1}{2}$×2a×($\sqrt{3}$a+h)=$\frac{3\sqrt{3}{a}^{2}}{2}$,
∴h=$\frac{\sqrt{3}a}{2}$.
∵ED∥AB,
∴△NPD∽△NAM,
∴$\frac{PD}{AM}$=$\frac{h}{h+\sqrt{3}a}$,即$\frac{PD}{2a}$=$\frac{\frac{\sqrt{3}a}{2}}{\frac{\sqrt{3}a}{2}+\sqrt{3}a}$,解得PD=$\frac{2a}{3}$,
∴PE=$\frac{1}{3}$a,
∴EP:OD=1:2.
故答案为:1:2.
点评 本题考查的是相似三角形的判定与性质,根据题意作出辅助线,利用正六边形的性质及锐角三角函数的定义求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
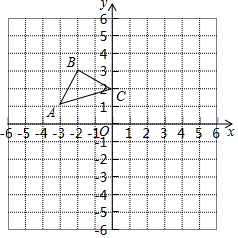 如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.
如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com