
 ��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D����AC=b��BC=a��AB=c��CD=h������������˵������a•b=c•h����a+b��c+h������a+b��h��c+hΪ�ߵ������Σ���ֱ�������Σ���$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$��������ȷ���У�������
��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D����AC=b��BC=a��AB=c��CD=h������������˵������a•b=c•h����a+b��c+h������a+b��h��c+hΪ�ߵ������Σ���ֱ�������Σ���$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$��������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� �ٸ��������������ʽ������⣻
��֤����a+b��2����c+h��2��
��ֱ�������Σ�֤����a+h��2+h2=��c+h��2��
��ֻ��֤��h2��$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$��=1��������Ƶ����ұߣ�
��� �⣺�١�Rt��ABC�����Ϊ��$\frac{1}{2}$ab��$\frac{1}{2}$ch��
��ab=ch���ʢ���ȷ��
�ڡ�c2��c2+h2��a2+b2=c2��
��a2+b2��c2+h2��
��ab=ch��
��a2+b2+2ab��c2+h2+2ch��
�ࣨa+b��2����c+h��2��
��a+b��c+h���ʢ���ȷ��
�ۡߣ�c+h��2=c2+2ch+h2��
h2+��a+b��2=h2+a2+2ab+b2��
��a2+b2=c2�������ɶ�����
ab=ch�������ʽ�Ƶ���
��c2+2ch+h2=h2+a2+2ab+b2��
�ࣨc+h��2=h2+��a+b��2��
����ݹ��ɶ������涨��֪��
��h��c+h��a+bΪ�߹��ɵ���������ֱ�������Σ�����ȷ��
�ܡ�ab=ch��
�ࣨab��2=��ch��2����a2b2=c2h2��
��a2+b2=c2��
��a2b2=��a2+b2��h2��
��$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=h2��
��$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{h}^{2}}$��
��$\frac{{a}^{2}}{{a}^{2}{b}^{2}}$+$\frac{{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{h}^{2}}$��
��$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$���ʢ���ȷ��
��ѡ��D��
���� ������Ҫ����ѧ���Թ��ɶ������ɶ������涨������������գ�������һ���İθ��Ѷȣ��������⣬��֤�������У�ע�������ϵʽab=ch��Ӧ�ã�


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ܳ�����16�� | B�� | �ܳ���С16�� | C�� | �������16�� | D�� | �����С16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���壺��ͼ����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ������ι���һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣬��AM=2��MN=3����BN�ij�Ϊ��������
���壺��ͼ����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ������ι���һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣬��AM=2��MN=3����BN�ij�Ϊ��������| A�� | $\sqrt{5}$ | B�� | $\sqrt{13}$ | C�� | $\sqrt{5}$��$\sqrt{13}$ | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
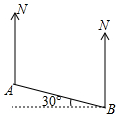 A��B���ص�λ����ͼ��ʾ����A��B�ģ�������
A��B���ص�λ����ͼ��ʾ����A��B�ģ�������| A�� | ��ƫ��30�� | B�� | ��ƫ��60�� | C�� | ��ƫ��30�� | D�� | ��ƫ��60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com