
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
【答案】
(1)解:AB=AC,理由如下:
连接OB.
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC

(2)解:延长AP交⊙O于D,连接BD,
设圆半径为r,则OP=OB=r,PA=5﹣r,
则AB2=OA2﹣OB2=52﹣r2,
AC2=PC2﹣PA2= ![]() ﹣(5﹣r)2,
﹣(5﹣r)2,
∴52﹣r2= ![]() ﹣(5﹣r)2,
﹣(5﹣r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:PB= ![]() .
.
∴⊙O的半径为3,线段PB的长为 ![]()
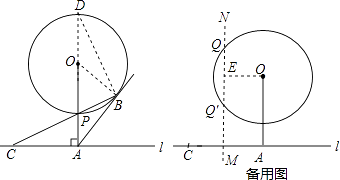
(3)解:作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE= ![]() AC=
AC= ![]() AB=
AB= ![]()
![]()
又∵圆O与直线MN有交点,
∴OE= ![]()
![]() ≤r,
≤r,
![]() ≤2r,
≤2r,
25﹣r2≤4r2,
r2≥5,
∴r≥ ![]() ,
,
又∵圆O与直线相离,
∴r<5,
即 ![]() ≤r<5
≤r<5
【解析】(1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5﹣r,根据AB=AC推出52﹣r2= ![]() ﹣(5﹣r)2 , 求出r,证△DPB∽△CPA,得出
﹣(5﹣r)2 , 求出r,证△DPB∽△CPA,得出 ![]() =
= ![]() ,代入求出即可;(3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案.
,代入求出即可;(3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如下两幅不完整的统计图.
(1)“从来不管”的问卷有份,在扇形图中“严加干涉”的问卷对应的圆心角为 .
(2)请把条形图补充完整.
(3)若该校共有学生2000名,请估计该校对手机问题“严加干涉”的家长有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是 ( )
A.0.96
B.0.95
C.0.94
D.0.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2小时,若船速为26千米/时,水速为3千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有2件上衣,分别为红色和蓝色,有3条裤子,其中2条为蓝色、1条为棕色.小明任意拿出1件上衣和1条裤子穿上.请用画树状图或列表的方法列出所有可能出现的结果,并求小明穿的上衣和裤子恰好都是蓝色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236)
≈2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. 
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是(用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解 如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角?(填“是”或“不是”).
(2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角. 请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com