
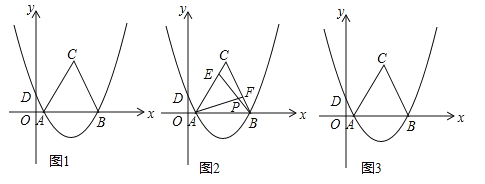
����Ŀ����ͼ1��������![]() ������A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱߡ�ABC��
������A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱߡ�ABC��
��1���������ߵĽ���ʽ��
��2����x���Ϸ������������Ƿ���ڵ�M����S��ABM=![]() S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2��E���߶�AC�ϵĶ��㣬F���߶�BC�ϵĶ��㣬AF��BE�ཻ�ڵ�P��
����CE=BF���Բ���AF��BE��������ϵ����APB�Ķ�������˵�����ɣ�
����AF=BE������E��A�˶���Cʱ����ֱ��д����P������·����������Ҫд���̣���
���𰸡���1��![]() ����2����M������Ϊ��9��4����1��4������3����AF=BE����APB=120�㣻��
����2����M������Ϊ��9��4����1��4������3����AF=BE����APB=120�㣻��![]() ��
��![]() ��
��
���������⣺��1���������⣬���������ߵĽ���ʽΪy=ax2+bx+![]() ��
��
�߽���A��B���������ã� 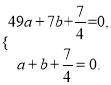 ��ã�a=
��ã�a=![]() ��b=��2��
��b=��2��
�������ߵĽ���ʽΪy=![]() x2��2x+
x2��2x+![]() ��
��
��2�����ڵ�M��ʹ��S��AMB=![]() S��ABC��
S��ABC��
���ɣ���ͼ��ʾ������C��CK��x�ᣬ����ΪK��
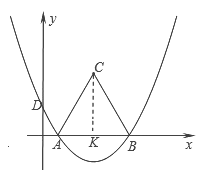
�ߡ�ABCΪ�ȱ������Σ�
��AB=BC=AC=6����ACB=60�㣮
��CK��AB��
��KA=BK=3����ACK=30�㣮
��CK=3![]() ��
��
��S��ABC=![]() ABCK=
ABCK=![]() ��6��3
��6��3![]() =9
=9![]() ��
��
��S��ABM=![]() ��
��![]() =12��
=12��
��M��a��![]() a2��2a+
a2��2a+![]() ����
����
��![]() AB|yM|=12����
AB|yM|=12����![]() ��6����
��6����![]() a2��2a+
a2��2a+![]() ��=12��
��=12��
���![]() =9��
=9�� ![]() =��1��
=��1��
��M1��9��4����M2����1��4����
��3���ٽ��ۣ�AF=BE����APB=120�㣮
���ɣ���ͼ��ʾ��
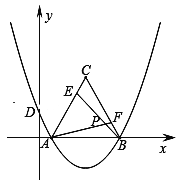
�ߡ�ABCΪ�ȱ������Σ�
��BC=AB����C=��ABF��
���ڡ�BEC�͡�AFB�У� 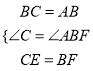 ��
��
���BEC�ա�AFB��
��AF=BE����CBE=��BAF��
���FAB+��ABP=��ABP+��CBE=��ABC=60�㣮
���APB=180�㩁��PAB����ABP=180�㩁60��=120�㣮
�ڵ�P������·����Ϊ![]() ��3
��3![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽ��ABCD����ͼ��ʾ�۵������۵��ǡ�FEC=64�㣮 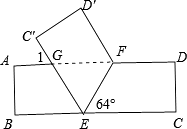
��1�����1�Ķ�����
��2����֤����EFG�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��B��C��D��ͬһ��ֱ���ϣ���ABC�͡�CDE���ǵȱ������Σ�BE��AC��F��AD��CE��H��
�١�BCE�ա�ACD��
��CF=CH��
�ۡ�CFHΪ�ȱ������Σ�
��FH��BD��
��AD��BE�ļн�Ϊ60�㣬
���Ͻ�����ȷ���� �� 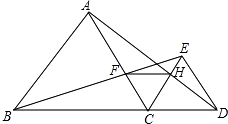
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A(2��0)����B (0��1)������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC������ACP��AP����![]() ��ʹ��C���ڵ�D��������A��D��PΪ���������������ABP���ƣ�����������������ĵ�P������Ϊ___________________________��
��ʹ��C���ڵ�D��������A��D��PΪ���������������ABP���ƣ�����������������ĵ�P������Ϊ___________________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
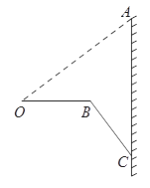
����Ŀ����ͼ�������г���λ�����С��������ʱ���Խ��Ƶؿ�������洹ֱ��չ��С���������ᱣ��ˮƽ����ͼ��ʵ����С����չ�����ʾ��ͼ������OB��ʾС����Ŀ��ȣ�BC��ʾС�����֧�ܣ�����OA����ʱOA=75���ף���AOB=��ACB=37������֧�ܳ�BC�������OB�ij���֮�͵���OA�ij��ȣ����B��AC�ľ��룮���ο����ݣ� ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=30�㣬��M��N�ֱ�������OA��OB�ϵĶ��㣬OPƽ�֡�AOB����OP=6����PMN���ܳ���СֵΪ �� 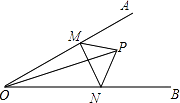
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=30�㣬��M��N�ֱ�������OA��OB�ϵĶ��㣬OPƽ�֡�AOB����OP=6����PMN���ܳ���СֵΪ �� 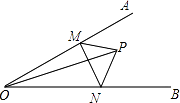
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̨��Ϥ���������콵ˮ������80%�����Դ���Ϣ�����漸��˵����ȷ������ ��
A. �������콫��80%�ĵ�����ˮ B. �������콫��80%��ʱ�併ˮ
C. ����϶����� D. ���콵ˮ�Ŀ����Դ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com