
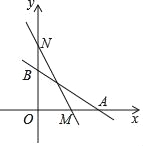
【题目】如图,直线:y=﹣![]() x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
(1)点B的坐标为 ;
(2)求△MNO的面积S与移动时间t之间的函数关系式;
(3)当t= 时,△NOM≌△AOB;
(4)若M在x轴正半轴上,且△NOM≌△AOB,G是线段ON上一点,连结MG,将△MGN沿MG折叠,点N恰好落在x轴上的H处,求G点的坐标.
【答案】(1)(0,2)(2)S=|8﹣2t|(3)2或6(4)(0,![]() ﹣1)
﹣1)
【解析】
(1)由点A的坐标利用待定系数法可求出b值,再利用一次函数图象上点的坐标特征可求出点B的坐标;
(2)由点A、H的坐标及点M移动的速度可得出ON、OM的长度,再利用三角形的面积公式即可找出△MNO的面积S与移动时间t之间的函数关系式;
(3)由OA=ON=4、∠AOB=∠NOM=90°,可得出若要△NOM≌△AOB只需OM=OB=2,结合OM=|4﹣t|可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(4)设点G的坐标为(0,y),则OG=y,由折叠的性质可找出GH、OH的长度,在Rt△GOH中,利用勾股定理可得出关于y的一元一次方程,解之即可得出结论.
(1)∵直线y=﹣![]() x+b过点A(4,0),
x+b过点A(4,0),
∴0=﹣![]() ×4+b,解得:b=2,
×4+b,解得:b=2,
∴直线AB的函数关系式为y=﹣![]() x+2.
x+2.
当x=0时,y=﹣![]() x+2=2,
x+2=2,
∴点B的坐标为(0,2).
故答案为:(0,2).
(2)∵A(4,0),N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动,
∴OA=4,ON=4,OM=OA﹣AM=|4﹣t|,
∴S=![]() OMON=
OMON=![]() |4﹣t|×4=|8﹣2t|.
|4﹣t|×4=|8﹣2t|.
(3)∵OA=ON=4,∠AOB=∠NOM=90°,
∴若要△NOM≌△AOB,只需OM=OB=2.
∵OM=|4﹣t|,
∴|4﹣t|=2,
解得:t=2或6.
故答案为:2或6.
(4)设点G的坐标为(0,y),则OG=y.
根据折叠的性质,可知:MH=MN=![]() =2
=2![]() ,GH=GN=4﹣y,
,GH=GN=4﹣y,
∴OH=2![]() ﹣2.
﹣2.
在Rt△GOH中,GH2=OG2+OH2,即(4﹣y)2=y2+(2![]() ﹣2)2,
﹣2)2,
解得:y=![]() ﹣1,
﹣1,
∴点G的坐标为(0,![]() ﹣1).
﹣1).


科目:初中数学 来源: 题型:
【题目】2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.
(1)第一批脐橙每件进价多少元?
(2)陈老板以每件120元的价格销售第二批脐橙,售出60%后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
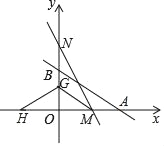
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
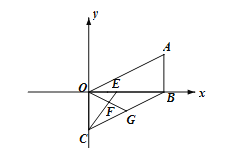
【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足![]() +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中, ![]() 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4 个小长方形,然后按图2的形状拼成一个正方形.

(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<![]() 的解集(请直接写出答案).
的解集(请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com