
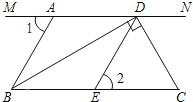
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
【答案】(1)AB∥DE,理由见解析;(2)见解析.
【解析】(1)首先根据平行线的性质,两直线平行,内错角相等即可证得∠ABC=∠1=60°,进而证明∠ABC=∠2,根据同位角相等,两直线平行,即可证得;
(2)①根据平行线的性质,两直线平行,同旁内角互补求得∠NDE的度数,然后根据角平分线的定义,以及平行线的性质即可求得∠C的度数,从而判断;
②在直角△BCD中,求得∠DBC的度数,然后求得∠ABD的度数,即可证得.
(1)AB∥DE,理由如下:
∵MN∥BC( 已知 ),
∴∠ABC=∠1=60°( 两直线平行,内错角相等 ).
又∵∠1=∠2( 已知 ).
∴∠ABC=∠2( 等量代换 ).
∴AB∥DE( 同位角相等,两直线平行 );
(2)①∵MN∥BC,
∴∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°.
∵DC 是∠NDE 的平分线,
∴∠EDC=∠NDC=![]() ∠NDE=60°.
∠NDE=60°.
∵MN∥BC,
∴∠C=∠NDC=60°.
∴∠ABC=∠C.
②∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°.
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.
∵MN∥BC,
∴∠DBC=∠ADB=30°.
∴∠ABD=∠DBC=![]() ∠ABC.
∠ABC.
∴BD 是∠ABC 的平分线.


科目:初中数学 来源: 题型:
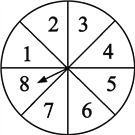
【题目】如图所示,转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.
(1)自由转动转盘,当它停止转动时,指针指向的数正好能整除8的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为![]() .(注:指针指在边缘处,要重新转,直至指到非边缘处)
.(注:指针指在边缘处,要重新转,直至指到非边缘处)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示. 为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )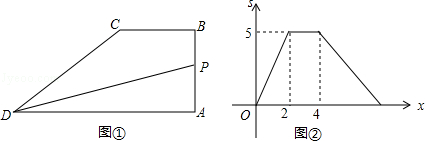
A.4
B.2+ ![]()
C.5
D.4+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
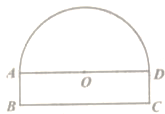
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.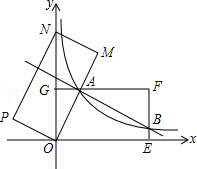
(1)求图象经过点A的反比例函数的解析式;
(2)设(2)中的反比例函数图象交EF于点B,直接写出直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 
(1)求证:BD是⊙O的切线.
(2)若AB= ![]() ,E是半圆
,E是半圆 ![]() 上一动点,连接AE,AD,DE. 填空:
上一动点,连接AE,AD,DE. 填空:
①当 ![]() 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 ![]() 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com