练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？

    【答案】解：∵小球滚动的速度与机器人行走的速度相等，

    ∴BC=AC，

    设BC=AC=xcm，

    则OC=（90﹣x）cm，

    在Rt△BOC中，

    ∵OB2+OC2=BC2，

    ∴302+（90﹣x）2=x2，

    解得x=50．

    答：机器人行走的路程BC为50cm


    【解析】由小球滚动的速度与机器人行走的速度相等，得出BC=AC=x，表示出OC的长，在Rt△BOC中，利用勾股定理，建立方程求解即可。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】9的平方根是（ ）

    A. 3 B. －3 C. ±3 D. ±6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠1与∠2是两条直线被第三条直线所截形成的同位角，若∠1=60°，则∠2为（ ）
    A.160°
    B.120°
    C.60°或120
    D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

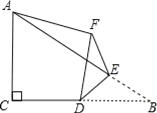
    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF的长取最小值时，BF的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求下列各式中x的值:(1)x2+6=10 (2)2（x-1）3=16.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

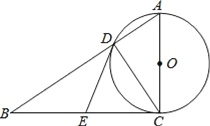
    【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O，与斜边AB交于点D、E为BC边的中点，连接DE．

    （1）求证：DE是⊙O的切线；

    （2）填空：①若∠B=30°，AC=2，则DE=　 　；

    ②当∠B=　 　°时，以O，D，E，C为顶点的四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（﹣1）2016+（3.14﹣π）0= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】浙江卫视《中国好声音》总决赛，全国有7100人通过电视收看，这个数据用科学记数法表示为（ ）
    A.71×102
    B.7.1×102
    C.7.1×103
    D.0.71×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B，C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．

    （1）求两次传球后，球恰在B手中的概率；

    （2）求三次传球后，球恰在A手中的概率.

    查看答案和解析>>

    同步练习册答案