
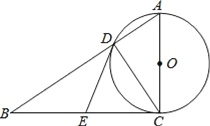
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2![]() ,则DE= ;
,则DE= ;
②当∠B= °时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)证明就解析;(2)①3;②45.
【解析】试题分析:(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;
(2)①直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长;
②当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
试题解析:(1)连接OD.
∵AC是直径,∴∠ADC=90°,∴∠CDB=90°,
又∵E为BC边的中点,∴DE为直角△DCB斜边的中线,∴DE=CE=![]() .∴∠DCE=∠CDE,
.∴∠DCE=∠CDE,
∵OC=OD,∴∠OCD=∠ODC,∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,∴∠ODE=90°
∴DE是⊙O的切线.
(2)①∵∠B=30°,AC=2![]() ,∠BCA=90°,∴tan30°=
,∠BCA=90°,∴tan30°=![]() =
=![]() ,解得:BC=6,
,解得:BC=6,
则DE=![]() BC=3;
BC=3;
故答案为:3;
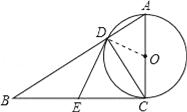
②当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,∴∠A=45°,
∵OA=OD,∴∠ADO=45°,∴∠AOD=90°,∴∠DOC=90°,
∵∠ODE=90°,∴四边形DECO是矩形,
∵OD=OC,∴矩形DECO是正方形.
故答案为:45.


科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)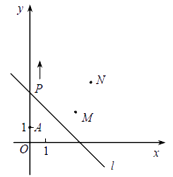
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com