
分析 作DM⊥BC于M,EN⊥BC于N,FH⊥BC于H,得到DM∥FG∥EN,得到MH=NH,根据等边三角形的性质得到∠B=∠C=60°,解直角三角形得到FH=$\frac{1}{2}$(DM+EN)=$\frac{7\sqrt{3}}{2}$,根据勾股定理即可得到结论.
解答 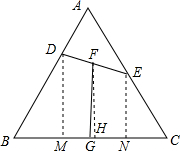 解:作DM⊥BC于M,EN⊥BC于N,FH⊥BC于H,
解:作DM⊥BC于M,EN⊥BC于N,FH⊥BC于H,
则DM∥FG∥EN,
∵DF=EF,
∴MH=NH,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵BD=8,CE=6,
∴BM=4,CN=3,DM=4$\sqrt{3}$,EN=3$\sqrt{3}$,
∴FH=$\frac{1}{2}$(DM+EN)=$\frac{7\sqrt{3}}{2}$,
∵BG=CG,BM-CN=1,
∴GN-GM=1,
∴GH=$\frac{1}{2}$,
∴FG=$\sqrt{F{H}^{2}+G{H}^{2}}$=$\sqrt{(\frac{7\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}$=$\sqrt{37}$.
故答案为:$\sqrt{37}$.
点评 本题考查了等边三角形的性质,梯形的中位线的性质,勾股定理,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.1}$ | B. | $\sqrt{8}$ | C. | $\sqrt{{x^2}+{x^2}y}$ | D. | $\sqrt{{x^2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
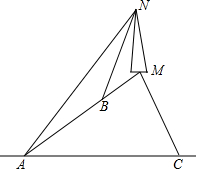 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或$\frac{9}{4}$ | D. | -1或-$\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com