

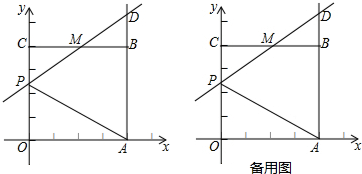
·ЦОц ЈЁ1Ј©Б¬ҪУACәНBDЈ¬Ҫ»УЪөгMЈ¬ЙиЎСPөДФІРДЧшұкКЗЈЁxЈ¬yЈ©Ј¬БРіцФІРДөҪMөД№ШПөКҪЈ¬°СP1ЈЁ0Ј¬2Ј©Ј¬P2ЈЁ-2Ј¬4Ј©Ј¬P3ЈЁ4$\sqrt{2}$Ј¬2Ј©ҙъИлЈ¬ҝҙКЗ·сіЙБўАҙЕР¶ЁЈ»
ЈЁ2Ј©°СөгPөДЧшұкҙъИлЈЁ1Ј©ЦРФІөД·ҪіМҝЙТФЗуөГЖд°лҫ¶Ј»ИзҙрНј2Ј¬ХТөҪХэ·ҪРОABCDөДЦРРДEЈ¬ёщҫЭөгPЎўBЎўEөДЧшұкНЖЦӘХвИэөгІ»№ІПЯЈ¬УЙЦұПЯУлФІөДО»ЦГ№ШПөҪшРРҪвҙрЈ»
ЈЁ3Ј©ўЩБ¬ҪУDHЈ¬ЧчDTЎНHFЈ¬ТФDОӘФІРДЈ¬DEОӘ°лҫ¶ЧчФІЈ¬Ҫ»DTУЪөгE1Ј¬Ҫ»HDУЪE2Ј¬өұ0ЈјrЈјDT-DE1КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®өұrЈҫHE2КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®ҫЭҙЛЗуҪвЈ®
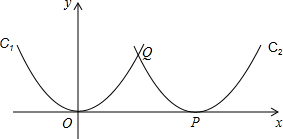
ўЪПИЗуіцЎчLIEОӘөИСьЦұҪЗИэҪЗРОЈ¬өГөҪLЈЁ0Ј¬5Ј©Ј¬Ҫш¶шөГіцЎчLOMОӘөИСьЦұҪЗИэҪЗРОЈ¬ЙиPЈЁpЈ¬-p+5Ј©ҫЭ№ШПөБРіц·ҪіМЗуБЛФІРДөДЧшұкЈ®
Ҫвҙр 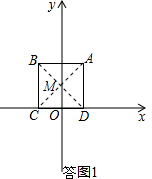 ҪвЈәЈЁ1Ј©ИзҙрНј1Ј¬Б¬ҪУACәНBDЈ¬Ҫ»УЪөгMЈ¬
ҪвЈәЈЁ1Ј©ИзҙрНј1Ј¬Б¬ҪУACәНBDЈ¬Ҫ»УЪөгMЈ¬
ЎЯЛДұЯРОABCDКЗХэ·ҪРОЈ¬
ЎаMөҪХэ·ҪРОABCDЛДМхұЯҫаАл¶јПаөИЈ¬
ЎаЎСPТ»¶ЁНЁ№эөгMЈ¬
ЎЯAЈЁ2Ј¬4Ј©
ЎаMЈЁ0Ј¬2Ј©
ЙиЎСPөДФІРДЧшұкКЗЈЁxЈ¬yЈ©Ј¬
Ўаr=2$\sqrt{2}$КұЈ¬
Ўаx2+ЈЁy-2Ј©2=ЈЁ2$\sqrt{2}$Ј©2Ј¬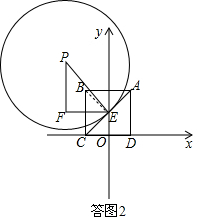
јҙЈ¬x2+ЈЁy-2Ј©2=8Ј¬
°СP1ЈЁ0Ј¬2Ј©Ј¬P2ЈЁ-2Ј¬4Ј©Ј¬P3ЈЁ4$\sqrt{2}$Ј¬2Ј©ҙъИлЈ¬Ц»УРP2Ј¬P4іЙБўЈ¬
ЎаҝЙТФіЙОӘХэ·ҪРОABCDөДЎ°өИҫаФІЎұөДФІРДөДКЗP2Ј¬P4Ј®
№Кҙр°ёКЗЈәP2Ј¬P4Ј®
ЈЁ2Ј©5Ј¬ЗТЎСPУлЦұПЯACөДО»ЦГ№ШПөКЗПаҪ»Ј®АнУЙИзПВЈә
°СPөгЧшұкЈЁ-3Ј¬6Ј©ҙъИлx2+ЈЁy-2Ј©2=ЈЁ-3Ј©2+ЈЁ6-2Ј©2=52Ј¬ФтёГФІөД°лҫ¶ОӘ5Ј®
ИзҙрНј2Ј¬ЙиХэ·ҪРОABCDөДЦРРДОӘEЈ¬ФтEЈЁ0Ј¬2Ј©Ј®
ЎЯPөгЧшұкОӘЈЁ-3Ј¬6Ј©Ј¬өгBөДЧшұкОӘЈЁ-2Ј¬4Ј©Ј¬
ЎаөгPЎўBЎўEІ»ФЪН¬Т»МхЦұПЯЙПЈ®
ЎЯЎПCEB=90ЎгЈ¬
ЎаЎПCEPЎЩ90ЎгЈ¬
ЎаөгPөҪACөДҫаАлұШРЎУЪ5Ј¬
ЎаЎСPУлЦұПЯACөДО»ЦГ№ШПөКЗПаҪ»Ј®
ЈЁ3Ј©ўЩИзҙрНј3Ј¬Б¬ҪУDHЈ¬ЧчDTЎНHFЈ¬ТФDОӘФІРДЈ¬DEОӘ°лҫ¶ЧчФІЈ¬Ҫ»DTУЪөгE1Ј¬Ҫ»HDУЪE2Ј¬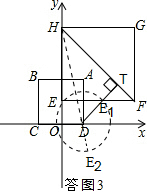 өұ0ЈјrЈјDT-DE1КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®
өұ0ЈјrЈјDT-DE1КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®
ЎЯHFЛщФЪөДЦұПЯОӘЈәy=-x+8Ј¬
DTЛщФЪөДЦұПЯОӘЈәy=x-2Ј¬
ЎаTЈЁ5Ј¬3Ј©Ј¬
ЎЯDЈЁ2Ј¬0Ј©Ј¬
ЎаDT=$\sqrt{{3}^{2}+ЈЁ5-2Ј©^{2}}$=3$\sqrt{2}$Ј¬
ЎЯDE=DE1
ЎаDT-DE1=DT-DE=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$Ј¬
Ўаөұ0ЈјrЈј$\sqrt{2}$КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®
өұrЈҫHE2КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®
ЎЯHE2=HD+DE2Ј¬DE2=DEЈ¬
ЎаHE2=HD+DE=$\sqrt{H{O}^{2}+O{D}^{2}}$+2$\sqrt{2}$=$\sqrt{{8}^{2}+{2}^{2}}$+2$\sqrt{2}$=2$\sqrt{17}$+2$\sqrt{2}$Ј¬
ЎаөұrЈҫ2$\sqrt{17}$+2$\sqrt{2}$КұЈ¬ПЯ¶ОHFЙПГ»УРТ»ёцөгДЬіЙОӘЛьөДЎ°өИҫаФІЎұөДФІРДЈ®
ўЪЎЯЎСPН¬КұОӘХэ·ҪРОABCDУлХэ·ҪРОEFGHөДЎ°өИҫаФІЎұЈ¬
ЎаЎСPН¬Кұ№эХэ·ҪРОABCDөД¶ФіЖЦРРДEәНХэ·ҪРОEFGHөД¶ФіЖЦРРДIЈ®
ЎаөгPФЪПЯ¶ОEIөДЦРҙ№ПЯЙПЈ®
ЎЯAЈЁ2Ј¬4Ј©Ј¬Хэ·ҪРОABCDөДұЯCDФЪxЦбЙПЈ»FЈЁ6Ј¬2Ј©Ј¬Хэ·ҪРОEFGHөДұЯHEФЪyЦбЙПЈ¬
ЎаEЈЁ0Ј¬2Ј©Ј¬IЈЁ3Ј¬5Ј©
ЎаЎПIEH=45ЎгЈ¬
ЙиПЯ¶ОEIөДЦРҙ№ПЯУлyЦбҪ»УЪөгLЈ¬УлxЦбҪ»УЪөгMЈ¬
ЎаЎчLIEОӘөИСьЦұҪЗИэҪЗРОЈ¬LIЎНyЦбЈ¬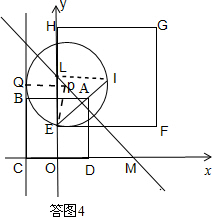
ЎаLЈЁ0Ј¬5Ј©Ј¬
ЎаЎчLOMОӘөИСьЦұҪЗИэҪЗРОЈ¬LO=OM
ЎаMЈЁ5Ј¬0Ј©Ј¬
ЎаPФЪЦұПЯy=-x+5ЙПЈ¬
ЎаЙиPЈЁpЈ¬-p+5Ј©
№эPЧчPQЎНЦұПЯBCУЪQЈ¬Б¬ҪбPEЈ¬
ЎЯЎСPУлBCЛщФЪЦұПЯПаЗРЈ¬
ЎаPE=PQЈ¬
Ўаp2+ЈЁ-p+5-2Ј©2=ЈЁp+2Ј©2Ј¬
ҪвөГЈәp1=5+2$\sqrt{5}$Ј¬p2=5-2$\sqrt{5}$Ј¬
ЎаP1ЈЁ5+2$\sqrt{5}$Ј¬-2$\sqrt{5}$Ј©Ј¬P2ЈЁ5-2$\sqrt{5}$Ј¬2$\sqrt{5}$Ј©Ј®
өгЖА ұҫМвҝјІйБЛФІЧЫәПМвЈ®Т»¶ЁТӘЕӘЗеіюМвёЙЦРөДТСЦӘМхјюЈ®ұҫМвЦРөДЎ°өИҫаФІЎұөД¶ЁТеКЗХэИ·ҪвМвөД№ШјьЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
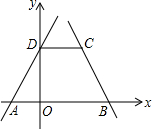 Т»ҙОәҜКэy=2x+2НјПуУлxЦбЎўyЦб·ЦұрҪ»УЪAЎўDБҪөгЈ¬Т»ҙОәҜКэy=-2x+8УлxЦбҪ»УЪBөгЈ¬№эDөгЧчDCЎОxЦбЈ¬Ҫ»ЦұПЯy=-2x+8УЪөгCЈ®
Т»ҙОәҜКэy=2x+2НјПуУлxЦбЎўyЦб·ЦұрҪ»УЪAЎўDБҪөгЈ¬Т»ҙОәҜКэy=-2x+8УлxЦбҪ»УЪBөгЈ¬№эDөгЧчDCЎОxЦбЈ¬Ҫ»ЦұПЯy=-2x+8УЪөгCЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
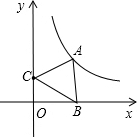 ИзНјЈ¬өгAКЗ·ҙұИАэәҜКэy=$\frac{5\sqrt{3}}{x}$ЈЁxЈҫ0Ј©НјПуЙПТ»өгЈ¬өгBКЗxЦбХэ°лЦбЙПТ»өгЈ¬өгCөДЧшұкОӘЈЁ0Ј¬2Ј©Ј¬өұЎчABCКЗөИұЯИэҪЗРОКұЈ¬өгAөДЧшұкОӘЈЁ$\frac{3\sqrt{3}}{5}$Ј¬$\frac{25}{3}$Ј©Ј®
ИзНјЈ¬өгAКЗ·ҙұИАэәҜКэy=$\frac{5\sqrt{3}}{x}$ЈЁxЈҫ0Ј©НјПуЙПТ»өгЈ¬өгBКЗxЦбХэ°лЦбЙПТ»өгЈ¬өгCөДЧшұкОӘЈЁ0Ј¬2Ј©Ј¬өұЎчABCКЗөИұЯИэҪЗРОКұЈ¬өгAөДЧшұкОӘЈЁ$\frac{3\sqrt{3}}{5}$Ј¬$\frac{25}{3}$Ј©Ј®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
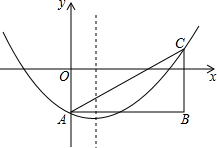 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЕЧОпПЯy=ax2-2ax-2ЈЁaЈҫ0Ј©УлyЦбҪ»УЪөгAЈ¬өгBөДЧшұкОӘЈЁ$\frac{1}{a}$Ј¬-2Ј©Ј¬№эөгBЧчyЦбөДЖҪРРПЯЈ¬Ҫ»ЕЧОпПЯУЪөгCЈ¬Б¬ҪбABЎўACЈ®
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЕЧОпПЯy=ax2-2ax-2ЈЁaЈҫ0Ј©УлyЦбҪ»УЪөгAЈ¬өгBөДЧшұкОӘЈЁ$\frac{1}{a}$Ј¬-2Ј©Ј¬№эөгBЧчyЦбөДЖҪРРПЯЈ¬Ҫ»ЕЧОпПЯУЪөгCЈ¬Б¬ҪбABЎўACЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
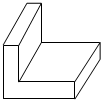 Т»ёцУГУЪ·АХрөДLРО°ьЧ°ЛЬБПЕЭДӯИзНјЛщКҫЈ¬ФтёГОпМеөДё©КУНјКЗЈЁЎЎЎЎЈ©
Т»ёцУГУЪ·АХрөДLРО°ьЧ°ЛЬБПЕЭДӯИзНјЛщКҫЈ¬ФтёГОпМеөДё©КУНјКЗЈЁЎЎЎЎЈ©| AЈ® |  | BЈ® |  | CЈ® | 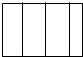 | DЈ® | 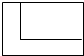 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | 32Ј¬31 | BЈ® | 31Ј¬32 | CЈ® | 31Ј¬31 | DЈ® | 32Ј¬35 |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com