练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．2010年3月份，某市市区一周空气质量报告中某项污染指数的数据是：31，35，31，34，30，32，31，这组数据的中位数、众数分别是（　　）
    A．32，31B．31，32C．31，31D．32，35

    分析 利用中位数及众数的定义确定答案即可．

    解答 解：∵数据31出现了3次，最多，
    ∴众数为31，
    ∵排序后位于中间位置的数是31，
    ∴中位数是31，
    故选C．

    点评 本题属于基础题，考查了确定一组数据的中位数、众数的能力．一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数的平均数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．对于一个圆和一个正方形给出如下定义：若圆上存在到此正方形四条边距离都相等的点，则称这个圆是正方形的“等距圆”
    如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．
    （1）当r=2$\sqrt{2}$时，在P1（0，2），P2（-2，4），P3（4$\sqrt{2}$，2）中可以成为正方形ABCD的“等距圆”的圆心的是P2，P4；
    （2）当P点坐标为（-3，6），则当⊙P的半径r=5时，⊙P是正方形ABCD的“等距圆”．试判断此时⊙P与直线AC的位置关系？并说明理由．
    （3）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上且点H在点E的上方．
    ①将正方形ABCD绕着点O旋转一周，在旋转的过程中，线段GF上没有一个点能称为它的“等距圆”的圆心，则r的取值范围是0＜r＜2$\sqrt{10}$-2或r＞12；
    ②若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P的圆心P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

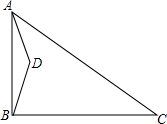    11．在△ABC中，∠ABC=90°，D为平面内一动点，AD=a，AC=b，其中a，b为常数，且a＜b．将△ABD沿射线BC方向平移，得到△FCE，点A、B、D的对应点分别为点F、C、E．连接BE．
    （1）如图，若D在△ABC内部，请在图中画出△FCE；
    （2）在（1）的条件下，若AD⊥BE，求BE的长（用含a，b的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若我们把十位上的数字比个位和百位上的数字都大的三位数称为凸数，如：786，465．则由1，2，3这三个数字构成的，数字不重复的三位数是“凸数”的概率是$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE=BF，EF=BD，且AD：DB=3：5，那么CF：CB等于（　　）
    A．3：5B．3：8C．5：8D．2：5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

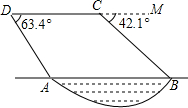    5．如图，某勘测飞机为了测量一湖泊两端A、B的距离，飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°，然后沿着平行于AB的方向水平飞行了125米，在点D测得端点B的俯角为42.1°，求湖泊A、B两端的距离．
    参考数据：tan63.4°≈2.00，sin63.4°≈0.89，cos63.4°≈0.45，tan42.1°≈0.90，sin42.1°≈0.67，cos42.1°≈0.74．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，在△ABC中，∠B=∠C，点D、E、F分别在AB、BC、AC上，且BD=CE，∠DEF=∠B，求证：△BDE≌△CEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知关于x的方程$\frac{x+a}{x+2}$=-1的根是负数，则a的取值范围是（　　）
    A．a＜0且a≠-2B．a＞0且a≠2C．a＞-2且a≠2D．a＜2且a≠-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．一只不透明的袋子中装有1个白球，2个黄球和3个红球，每个球除颜色外都相同，将球搅匀，从中任意摸出一个球．如果想使摸到这三种颜色的球的概率相等，下列做法正确的是（　　）
    A．向袋子里分别投放1个白球，1个黄球，1个红球
    B．向袋子里分别投放3个白球，2个黄球，1个红球
    C．向袋子里分别投放2个白球，1个红球
    D．向袋子里投放2个白球

    查看答案和解析>>

    同步练习册答案