
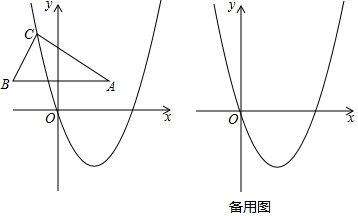
���� ��1������ֱ������������ǻ��������A=��BCD=30�㣬Ȼ�����ֱ��������30������Ե�ֱ�DZߵ���б�ߵ�һ�����BC��BD�������ù��ɶ�����ʽ���㼴�ɵý⣻
��2�����ݵ�B�������AB�ij��������A�����꣬�������C�����꣬Ȼ�����ô���ϵ��������κ�������ʽ���
��3����AB��BC��y��Ľ���ֱ�ΪE��F��Ȼ�����������ε�������BE���ٱ�ʾ��DE���Ӷ��õ���C�ĺ����꣬�ٸ��ݵ�C���������ϣ��ѵ�C�ĺ�����������������õ���C�������꼴�ɵý⣮
��4����ͼ2�У�������һ����PMN�ա�CBA����P���C��Ӧ����������ڡ�PMN�ա�CBA����PH��MN��H���������M�����꣬�������P�����֤꣬����P���������ߵ�ͼ���ϣ����ɽ�����⣮
��� �⣺��1���ߡ�CAB=60�㣬CD��б��AB�ϵĸߣ�
���B=��ACD=90��-60��=30�㣬
��AC=$\frac{1}{2}$AB=$\frac{1}{2}$��8=4��
AD=$\frac{1}{2}$AC=$\frac{1}{2}$��4=2��
��Rt��ACD��CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$��
�ʴ�Ϊ2$\sqrt{3}$��
��2���ߵ�B�����ǣ�-3��0����AB=8��
���A�������� 5��0����
��OB=3��BD=2��
���C��������-1��2$\sqrt{3}$����
�ߵ�A�� 5��0����C��-1��2$\sqrt{3}$������������y=ax2+bx�ϣ�
��$\left\{\begin{array}{l}{25a+5b=0}\\{a-b=2\sqrt{3}}\end{array}\right.$��
��� $\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{5\sqrt{3}}{3}}\end{array}\right.$��
���ԣ������߽���ʽΪy=$\frac{\sqrt{3}}{3}$x2-$\frac{5\sqrt{3}}{3}$x��
��3����ͼ1�У���AB��BC��y��Ľ���ֱ�ΪE��F��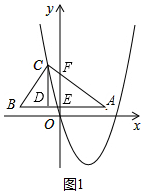
��EF=AE•tanA=$\frac{\sqrt{3}}{3}$AE��
��Rt��ABC��y��ֳ������֣�
��$\frac{1}{2}$AE•EF=$\frac{1}{2}$��$\frac{1}{2}$AB•CD��
�� $\frac{1}{2}$AE•$\frac{\sqrt{3}}{3}$AE=4$\sqrt{3}$��
��AE=2$\sqrt{6}$��
�֡�AD=AB-BD=8-2=6��
���C�ĺ�����Ϊ-��6-2$\sqrt{6}$��=-6+2$\sqrt{6}$��
�ߵ�C��������y=$\frac{\sqrt{3}}{3}$x2-$\frac{5\sqrt{3}}{3}$x�ϣ�
��y=$\frac{\sqrt{3}}{3}$��-6+2$\sqrt{6}$��2-$\frac{5\sqrt{3}}{3}$��-6+2$\sqrt{6}$��=30$\sqrt{3}$-34$\sqrt{2}$��
���ԣ���C������Ϊ��-6+2$\sqrt{6}$��30$\sqrt{3}$-34$\sqrt{2}$����
��4����ͼ2�У�������һ����PMN�ա�CBA����P���C��Ӧ�����������£�
������ڡ�PMN�ա�CBA����PH��MN��H��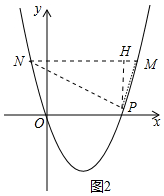
�������߽���ʽΪy=$\frac{\sqrt{3}}{3}$x2-$\frac{5\sqrt{3}}{3}$x�ĶԳ���x=$\frac{5}{2}$��
��MN=AB=8��
���M�ĺ�����Ϊ$\frac{5}{2}$+4=$\frac{13}{2}$��
���M��������Ϊ$\frac{\sqrt{3}}{3}$����$\frac{13}{2}$��2-$\frac{5\sqrt{3}}{3}$��$\frac{13}{2}$=$\frac{13\sqrt{3}}{4}$��
��M��$\frac{13}{2}$��$\frac{13\sqrt{3}}{4}$����
�ߡ�PMN�ա�CBA��
��PH=2$\sqrt{3}$HM=2��
��P��$\frac{9}{2}$��$\frac{5\sqrt{3}}{4}$����
����������y=$\frac{\sqrt{3}}{3}$x2-$\frac{5\sqrt{3}}{3}$x����x=$\frac{9}{2}$ʱ��y=$\frac{\sqrt{3}}{3}$����$\frac{9}{2}$��2-$\frac{5\sqrt{3}}{3}$��$\frac{9}{2}$=$\frac{3\sqrt{3}}{4}$��
���P���������ߵ�ͼ���ϣ�
�����һ����PMN�ա�CBA��
���� �����Ƕ��κ����ۺ����ͣ���Ҫ������ֱ������������ǻ�������ʣ����ɶ�����Ӧ�ã�����ϵ��������κ�������ʽ�����κ���ͼ���ϵ��������������2����ʾ����C�ĺ������ǽ���Ĺؼ�����3���ѵ��������������ε���������B��y��ľ��룬��BE�ij��ȣ���4���ؼ��Ǽ�����ڣ������P�����꣬�жϵ�P�Ƿ��������ߵ�ͼ���ϼ��ɣ��������Ѷȣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
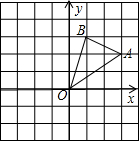 ��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��2����B��1��3��
��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��2����B��1��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 4��-10 | C�� | -10 | D�� | 10��-4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com