练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，在平行四边形ABCD中，AD=AC，∠B=65°，DE⊥AC于E，则∠EDC=25°．

    分析 在Rt△DEC中，想办法求出∠DCE即可解决问题．

    解答 解：∵四边形ABCD是平行四边形，
    ∴∠B=∠ADC=65°，
    ∵AD=AC，
    ∴∠ADC=∠C=65°，
    ∵DE⊥AC，
    ∴∠DEC=90°，
    ∴∠EDC=90°-∠C=25°，
    故答案为25．

    点评 本题考查平行四边形的判定、等腰三角形的性质、直角三角形的性质等知识，解题的关键是利用平行四边形的性质以及等腰三角形的性质求出∠DCE，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上．
    （1）从A、D、E、F四个点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是直角三角形的概率是$\frac{3}{4}$；
    （2）从A、D、E、F四个点中先后任意取两个不同的点，以所取的这两点及点B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树状图或列表法求解）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

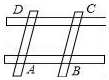    4．如图所示是由四根木棒搭成的平行四边形框架，AB=8cm，AD=6cm，在这个位置，将AB固定，逆时针转动AD．则关于?ABCD面积S的变化描述正确的是（　　）
    A．保持不变B．先变小，再变大C．先变大，再变小D．0＜S＜48

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

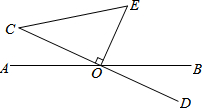    1．如图，AB，CD交于点O，OE⊥CD于O，连接CE，
    （1）若∠AOC=25°，则∠BOE=65°．
    （2）若OC=2cm．OE=1.5cm，CE=2.5cm，那么点E到直线CD的距离是1.5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知在平面直角坐标系中，四边形OABC的四个顶点坐标分别是O（0，0），A（0，3），B（5，4），C（4，0）．
    （1）在坐标系中画出四边形OABC，并求四边形OABC的面积．
    （2）连接线段AC，将线段AC向左平移m个单位长度，再向下平移n个单位长度，使得A的对应点A′恰好落在x轴上，C的对应点C′恰好落在y轴上，写出m和n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，边长为2菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第4个菱形的边长为6$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\sqrt{{{（\sqrt{3}-2）}^2}}$-$\sqrt{12}$+$\sqrt{27}$-$\frac{4}{{\sqrt{2}}}$+（$\frac{1}{2}}$）-1
    （2）$\sqrt{3}$×（3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：①∠DCF=$\frac{1}{2}$∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．其中一定成立的是①②④．（把所有正确结论的序号都填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在平面直角坐标系内，点P（25-5a，9-3a）关于y轴对称的点在第三象限，且a是整数，则点P的坐标是（5，-3）．

    查看答案和解析>>

    同步练习册答案