
 已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一条直线上,点A从点M开始向右移动,设点A的移动距离为xcm(0≤x≤20),重叠部分的面积为S(cm2).
已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一条直线上,点A从点M开始向右移动,设点A的移动距离为xcm(0≤x≤20),重叠部分的面积为S(cm2).分析 (1)当x=4cm时,AM=4,根据三角形的面积公式即可得出S的值;
(2)当10cm<x≤20cm时,则AN=x-10,利用分割图象求面积法结合三角形的面积即可得出S关于x的函数关系式.
解答 解:(1)当x=4cm时,AM=4,
重叠部分的面积S=$\frac{1}{2}$AM2=$\frac{1}{2}$×4×4=8(cm2).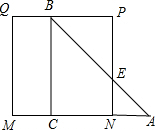
(2)当10cm<x≤20cm时,如图所示.
AN=x-MN=x-10,
∴S=S△ABC-S△ANE=$\frac{1}{2}$AC2-$\frac{1}{2}$AN2=$\frac{1}{2}$×102-$\frac{1}{2}$(x-10)2=-$\frac{1}{2}$x2+10x(10<x≤20).
故答案为:S=-$\frac{1}{2}$x2+10x(10<x≤20).
点评 本题考查了三角形的面积公式以及动点问题的函数图象,解题的关键是:(1)根据三角形的面积公式算出S的值;(2)利用分割图象求面积法找出S关于x的函数关系式.本题属于基础题,难度不大,解决该题型题目时,利用分割图象求面积法找出函数关系式是关键.


科目:初中数学 来源: 题型:解答题

| 白纸张数 | 1 | 2 | 3 | 4 | 5 | |
| 纸条长度 | 40 | 75 | 110 | 145 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com