
【题目】如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.
(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD,CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD,∴∠ABC-∠ABE=∠EBD-∠ABE,即∠EBC=∠DBA.在△EBC和△DBA中,
BC=BA,∠______=∠______,BE=BD,
∴△EBC≌△DBA,∴CE=AD,∠ECB=∠______.
∵∠ECB+∠ACE+∠CAB=90°,∴∠DAB+∠ACE+∠CAB=90°,∴∠______=90°,∴AD⊥EC.
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD,CE.问(1)中线段AD,EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD,CE.请说明AD,EC间的数量关系和位置关系.

【答案】 (1)EBC DBA DAB AKC
(2)成立,理由见解析;(3)AD=EC,AD⊥EC.
【解析】(1)根据证明过程直接填空即可;
(2)先证△ADB与△CBE全等,得出CE=AD,和∠ECB=∠DAB,延长CE交AD于点F,由于∠DAB与∠ADB互余,从而∠ECB也与∠ADB互余,从而得征;
(3)方法与(2)相同;
(1)∵∠ABC=∠EBD,
∴∠ABC﹣∠ABE=∠EBD﹣∠ABE即∠EBC=∠DBA,
在△EBC和△DBA中,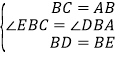 ,
,
∴△EBC≌△DBA,∴AD=EC,∠ECB=∠DAB.
∵∠ECB+∠ACE+∠CAB=90°,
∴∠DAB+∠ACE+∠CAB=90°,
∴∠AKC=90°,∴AD⊥EC.
(2)成立.理由如下:
如图3,延长CE交AD于F.
在△EBC和△DBA中, ,
,
∴△EBC≌△DBA,∴AD=EC,∠ECB=∠DAB.
∵∠DAB+∠ADB=90°,∴∠ECB+∠ADB=90°,∴AD⊥EC;
(3)AD=EC,AD⊥EC.理由如下:
如图4,设CE、AD交于点F,
∵∠DBE=∠ABC=90°,∴∠CBE=∠ABD.
在△EBC和△DBA中, ,
,
∴△EBC≌△DBA,∴AD=EC,∠CEB=∠ADB.
∵∠ADB+∠DFB=90°,∴∠CEB+∠AFE=90°,∴AD⊥EC.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称. 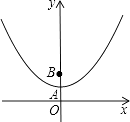
(1)填空:点B的坐标为;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元、25元,从B村运往C、D两处的费用分别为每吨15元、18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元、yB元.
(1)请填写下表,并求出yA、yB与x之间的函数表达式;

(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB,PQ是圆O的两条直径,连接PB,AQ.
(1)如图①,求证:AQ∥BP,AG∥BP; 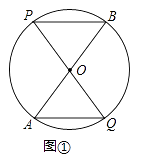
(2)如图②,过点B作BC⊥PQ于点D,交圆O于点C,在DG上取一点K,使DK=DP,求证:四边形AQKC是平行四边形. 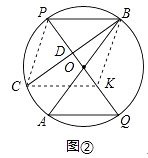
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( ) 
A.6
B.6.25
C.6.5
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类:
![]()
负整数集合:{____________________}
正分数集合:{____________________}
负分数集合:{____________________}
整数集合:{_______________________}
负有理数集合:{_______________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度. 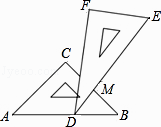
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图像如图所示,则方程ax2+(b﹣
x的图像如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com