

分析 (1)只要证明,$\frac{AC}{AD}$=$\sqrt{2}$,$\frac{AP}{AQ}$=$\sqrt{2}$,推出$\frac{AC}{AD}$=$\frac{AP}{AQ}$,再证明∠DAQ=∠CAP即可证明.
(2)由题意设正方形ABCD的边长为2a,则PB=PC=a,由△APE∽△ACP,推出$\frac{PE}{PC}$=$\frac{AP}{AC}$=$\frac{AE}{AP}$=$\frac{\sqrt{5}a}{2\sqrt{2}a}$=$\frac{\sqrt{10}}{4}$,推出AE=$\frac{5\sqrt{2}}{4}$a,PE=$\frac{\sqrt{10}}{4}$a,推出EC=AC-AE=$\frac{3\sqrt{2}}{4}$a,由PQ=$\frac{\sqrt{2}}{2}$AP=$\frac{\sqrt{10}}{2}$a,推出QE=PQ-PE=$\frac{\sqrt{10}}{4}$a,推出PE=QE=$\frac{\sqrt{10}}{4}$a,由此即可解决问题.
(3)由(2)可知n=2时,PE=QE.
(4)连接AC、DQ、BQ、作QM⊥AB于M,QN⊥BC于N.由(1)可知△ADQ∽△ACP,推出∠ADQ=∠ACP=45°,推出DQ平分∠ADC,由△AQM≌△PQN,推出MQ=QN,AM=PN,推出四边形MBNQ是正方形,推出BQ平分∠ABC,BM=BN,推出B、Q、D共线,设PB=a,AM=PN=m,则AB=BC=na,可得a+m=an-m,即m=$\frac{n-1}{2}$a,推出BM=BN=$\frac{n+1}{2}$a,BQ=$\sqrt{2}$BN=$\frac{\sqrt{2}}{2}$(n+1)a,由BD=$\sqrt{2}$na,推出DQ=BD-BQ=$\sqrt{2}$na-$\frac{\sqrt{2}}{2}$(n+1)a=$\frac{\sqrt{2}}{2}$(n-1)a,由DF∥PB,得$\frac{DF}{PB}$=$\frac{DQ}{BQ}$,求出DF即可解决问题.
解答 (1)证明:∵四边形ABCD为正方形,
∴∠DAC=45°,即∠DAQ+∠QAE=45°,$\frac{AC}{AD}$=$\sqrt{2}$,
∵△APQ为等腰直角三角形,
∴∠QAP=45°,即∠PAC+∠QAE=45°,$\frac{AP}{AQ}$=$\sqrt{2}$,
∴∠PAC=∠QAD,$\frac{AC}{AD}$=$\frac{AP}{AQ}$,
∴△ACP∽△ADQ;
(2)解:由题意设正方形ABCD的边长为2a,则PB=PC=a,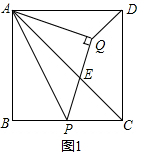
∴AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{(2a)^{2}+{a}^{2}}$=$\sqrt{5}$a,AC=2 $\sqrt{2}$a,
∵∠APE=∠ACP=45°,∠PAE=∠CAP,
∴△APE∽△ACP,
∴$\frac{PE}{PC}$=$\frac{AP}{AC}$=$\frac{AE}{AP}$=$\frac{\sqrt{5}a}{2\sqrt{2}a}$=$\frac{\sqrt{10}}{4}$,
∴AE=$\frac{5\sqrt{2}}{4}$a,PE=$\frac{\sqrt{10}}{4}$a,
∴EC=AC-AE=$\frac{3\sqrt{2}}{4}$a,
∵PQ=$\frac{\sqrt{2}}{2}$AP=$\frac{\sqrt{10}}{2}$a,
∴QE=PQ-PE=$\frac{\sqrt{10}}{4}$a,
∴PE=QE=$\frac{\sqrt{10}}{4}$a,
∴$\frac{CE}{AE}$=$\frac{\frac{3\sqrt{2}}{4}a}{\frac{5\sqrt{2}}{4}a}$=$\frac{3}{5}$,$\frac{PE}{QE}$=1.
(3)解:由(2)可知,n=2时,PE=EQ.
故答案为2.
(4)解:连接AC、DQ、BQ、作QM⊥AB于M,QN⊥BC于N.
由(1)可知△ADQ∽△ACP,
∴∠ADQ=∠ACP=45°,
∴DQ平分∠ADC,
∵∠QMB=∠MBN=∠QNB=90°,
∴四边形MBNQ是矩形,
∵∠MQN=∠AQP=90°,
∴∠AQM=∠PQN,∵∠AMQ=∠QNP=90°,AQ=PQ,
∴△AQM≌△PQN,
∴MQ=QN,AM=PN,
∴四边形MBNQ是正方形,
∴BQ平分∠ABC,BM=BN,
∴B、Q、D共线,设PB=a,AM=PN=m,则AB=BC=na,
∴a+m=an-m,
∴m=$\frac{n-1}{2}$a,
∴BM=BN=$\frac{n+1}{2}$a,BQ=$\sqrt{2}$BN=$\frac{\sqrt{2}}{2}$(n+1)a,
∵BD=$\sqrt{2}$na,
∴DQ=BD-BQ=$\sqrt{2}$na-$\frac{\sqrt{2}}{2}$(n+1)a=$\frac{\sqrt{2}}{2}$(n-1)a,
∵DF∥PB,
∴$\frac{DF}{PB}$=$\frac{DQ}{BQ}$,
∴$\frac{DF}{a}$=$\frac{\frac{\sqrt{2}}{2}(n-1)a}{\frac{\sqrt{2}}{2}(n+1)a}$,
∴DF=$\frac{n-1}{n+1}$a,
∴AF=AD-DF=na-$\frac{n-1}{n+1}$a=$\frac{{n}^{2}+1}{n+1}$a,
∴$\frac{DF}{AF}$=$\frac{\frac{n-1}{n+1}a}{\frac{{n}^{2}+1}{n+1}a}$=$\frac{n-1}{{n}^{2}+1}$.
故答案为$\frac{n-1}{{n}^{2}+1}$.
点评 本题考查了全等三角形的判定和性质、相似三角形的判定与性质、等腰直角三角形的性质、正方形的性质和判定、平行线分线段成比例定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数,探究线段之间的关系,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | x2+130x-1400=0 | B. | x2+65x-350=0 | C. | x2-130x-1400=0 | D. | x2-65x-350=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=1 | B. | (x-2)2=4 | C. | (x-2)2=3 | D. | (x-2)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
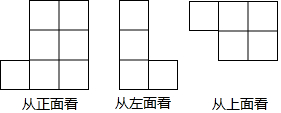
 用10米长的铝材制成一个面积为6平方米的窗框,窗框的形状如图所示,若设它的一条竖直方向的边长为x米,则所列方程为( )
用10米长的铝材制成一个面积为6平方米的窗框,窗框的形状如图所示,若设它的一条竖直方向的边长为x米,则所列方程为( )| A. | x(5-$\frac{3}{2}$x)=6 | B. | x(5-x)=6 | C. | x(10-$\frac{3}{2}$x)=6 | D. | x(10-3x)=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺.另一醉汉叫他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,你知道竹竿有多长吗?若设竹竿的长为x尺,则下列方程,满足题意的是( )
从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺.另一醉汉叫他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,你知道竹竿有多长吗?若设竹竿的长为x尺,则下列方程,满足题意的是( )| A. | (x+2)2+(x-4)2=x2 | B. | (x+2)2+(x+4)2=x2 | C. | (x-2)2+(x-4)2=x2 | D. | (x-2)2+(x+4)2=x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=4(x+2)2+3 | B. | y=4(x-2)2+3 | C. | y=4(x+3)2+2 | D. | y=4(x-3)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
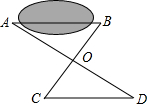 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )| A. | OA=OD,OB=OC | B. | ∠B=∠C,OB=OC | C. | ∠B=∠C,OA=OD | D. | ∠C=∠B,∠A=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com