
【题目】如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm。

求:(1)FC的长;
(2)EF的长。
【答案】(1)FC= 4cm;(2)EF=5cm.
【解析】试题分析:(1)根据折叠的性质可得AD=AF=10cm,在Rt△ABF中利用勾股定理计算出BF的长,进而得到FC的长;(2)由题意可得EF=DE,设DE=EF=xcm,则EC=(8-x)cm,在Rt△EFC中利用勾股定理可得(8-x)2+42=x2,再解方程即可得答案.
试题解析:
(1)由题意可得,AF=AD=10cm,在Rt△ABF中,∵AB=8,
∴BF=6cm,
∴FC=BC﹣BF=10﹣6=4cm;
(2)由题意可得EF=DE,可设DE的长为x,则在Rt△EFC中,(8﹣x)2+42=x2,解得x=5,即EF的长为5cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
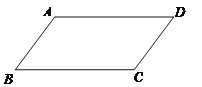
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件,只能画出唯一的△ABC的是( )
A. AB=3 BC=4 B. AB=4 BC=3 ∠A=30°
C. ∠A=60°∠B=45° AB=4 D. ∠C=60°AB=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )
A.(x﹣4)2=21
B.(x﹣4)2=11
C.(x+4)2=21
D.(x+4)2=11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下列长度的三条线段,能组成三角形的是( )
A.3cm,5cm,7cmB.7cm,7cm,14cmC.4cm,5cm,9cmD.2cm,1cm,3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
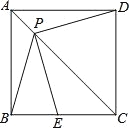
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在七年级数学联欢会上,教师出示了10张数学答题卡.答题卡背面的图案各不相同:当答题卡正面是正数时,背面是一面旗;当答题卡正面是负数时,背面是一朵花.这10张答题卡如下所示: ①(﹣4)×(﹣2)
②﹣2.8+(+1.9)
③0+(﹣12.9)
④﹣(﹣2)2
⑤﹣0.5÷(﹣2)
⑥|﹣3|﹣(﹣2)
⑦(﹣ ![]() )2×
)2× ![]()
⑧ ![]()
⑨4÷(19﹣59)
⑩a2+1
请你通过观察说出:答题卡后有几面旗?几朵花?并写出它们的序号.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com