
【题目】如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由. 
【答案】
(1)解:∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D
(2)解:如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.

【解析】(1)首先过点P作PE∥AB,由AB∥CD,可得PE∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠B,∠2=∠D,则可求得∠BPD=∠B+∠D.(2)由AB∥CD,根据两直线平行,内错角相等与三角形外角的性质,即可求得∠BPD与∠B、∠D的关系.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A. 直角的补角是直角
B. 两直线平行,一组同旁内角的角平分线互相垂直
C. 等腰三角形的高、中线、角平分线三线合一
D. 有两角及其中一角的平分线对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
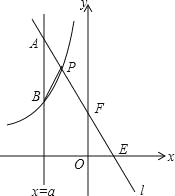
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师给同学们出了一道化简的题目:2(2x2y+x)﹣3(x2y﹣2x),小亮同学的做法如下:2(2x2y+x)﹣3(x2y﹣2x)=4x2y+x﹣3x2y﹣2x=x2y﹣x.请你指出小亮的做法正确吗?如果不正确,请指出错在哪?并将正确的化简过程写下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把命题“等角对等边”,改写成如果___________________________________________________那么______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com