
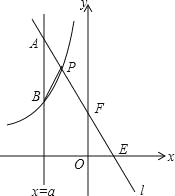
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
【答案】(1)y=﹣2x+2;(2)a=-2.
【解析】
试题分析:(1)先由y=![]() ,求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
,求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为﹣2a+2,B点的纵坐标为![]() ,D点的纵坐标为4,列出方程求解即可.
,D点的纵坐标为4,列出方程求解即可.
试题解析:(1)由P(﹣1,n)在y=![]() 上,得n=4,
上,得n=4,
∴P(﹣1,4),
∵F为PE中点,
∴OF=![]() n=2,
n=2,
∴F(0,2),
又∵P,F在y=kx+b上,
∴![]() ,解得
,解得![]() .
.
∴直线l的解析式为:y=﹣2x+2.
(2)如图,过P作PD⊥AB,垂足为点D,
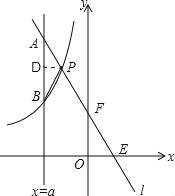
∵PA=PB,
∴点D为AB的中点,
又由题意知A点的纵坐标为﹣2a+2,B点的纵坐标为![]() ,D点的纵坐标为4,
,D点的纵坐标为4,
∴得方程﹣2a+2![]() =4×2,
=4×2,
解得![]() =﹣2,
=﹣2,![]() =﹣1(舍去).
=﹣1(舍去).
∴当a=﹣2时,PA=PB.


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,分别添加下列条件:①AB∥CD;②AB=CD;③AD=BC;④∠B=∠D;⑤∠A=∠C,其中能使四边形ABCD成为平行四边形的条件有( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋数学家杨辉曾提出这样一个问题:“直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步.”如果设矩形田地的长为x步,那么根据题意列出的方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )
A.(x﹣4)2=21
B.(x﹣4)2=11
C.(x+4)2=21
D.(x+4)2=11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com