
���� ��1��������֪���������˻��ĵ������ڸ��Ե����IJ�ݴ˿ɵã�
��2�����ݣ�1���й��ɿɵã�
��3�����ݣ�1���й��ɿɵã�
��4�����ã�1���й��ɽ������������������ɵã�
��� �⣺��1����1��ʽ��Ϊ$\frac{1}{1��2}$=1-$\frac{1}{2}$��
��2��ʽ��Ϊ��$\frac{1}{2��3}$=$\frac{1}{2}$-$\frac{1}{3}$��
��3��ʽ��Ϊ��$\frac{1}{3��4}$=$\frac{1}{3}$-$\frac{1}{4}$��
��4��ʽ��Ϊ��$\frac{1}{4��5}$=$\frac{1}{4}$-$\frac{1}{5}$��
��
���8��ʽ��Ϊ$\frac{1}{8��9}$=$\frac{1}{8}$-$\frac{1}{9}$��
��9��ʽ��Ϊ$\frac{1}{9��10}$=$\frac{1}{9}$-$\frac{1}{10}$��
��10��ʽ��Ϊ$\frac{1}{10��11}$=$\frac{1}{10}$-$\frac{1}{11}$��
�ʴ�Ϊ��$\frac{1}{8��9}$=$\frac{1}{8}$-$\frac{1}{9}$��$\frac{1}{9��10}$=$\frac{1}{9}$-$\frac{1}{10}$��$\frac{1}{10��11}$=$\frac{1}{10}$-$\frac{1}{11}$��
��2���ɣ�1��֪����2016����Ϊ$\frac{1}{2016��2017}$=$\frac{1}{2016}$-$\frac{1}{2017}$��
�ʴ�Ϊ��$\frac{1}{2016��2017}$=$\frac{1}{2016}$-$\frac{1}{2017}$��
��3����n��ʽ��Ϊ$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��
�ʴ�Ϊ��$\frac{1}{n��n+1��}$��$\frac{1}{n}$-$\frac{1}{n+1}$��
��4��ԭʽ=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+��+$\frac{1}{99}$-$\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$��
���� ������Ҫ�������ֵı仯���ɣ���������ó����������˻��ĵ������ڸ��Ե����IJ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ�����ȡ���ֱ��ƽ���ı����������� | |
| B�� | �Խ�����ȵ�ƽ���ı����Ǿ��� | |
| C�� | �Խ��ߴ�ֱ���ı��������� | |
| D�� | �Խ�����ƽ�ֵ��ı�����ƽ���ı��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
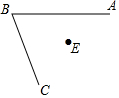 ��ͼ����ABC���ڲ���һ��E
��ͼ����ABC���ڲ���һ��E�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com